Аппаратура потребителей спутниковых радионавигационных систем (дисциплина)

Дисциплина "Аппаратура потребителей спутниковых радионавигационных систем" входит в вариативную часть общенаучного цикла занятий учебного плана подготовки специалистов по направлению 11.05.01 "Радиоэлектронные системы и комплексы".

Преподается осеннем и весеннем семестрах пятого года обучения. В осеннем семестре лекции и лабораторные занятия (итог - экзамен), в весеннем - курсовой проект.

По дисциплине подготовлен электронный учебно-методический комплекс.

Календарный план

Неделя	Дата	Лекция	Лабораторная	Контрольное мероприятие
1	07.09	Основы СРНС. Сегменты СРНС. Методы позиционирования.	Ошибки позиционирования в городских условиях
2	14.09	Навигационные сигналы.
3	21.09	Антенна, МШУ		КМ-1: Модель сигнала ГНСС
4	25.09	Радиочастотный блок (Аналогово-цифровое преобразование. Синтезатор частот. План частот АП СРНС. )
5	02.10	Математическая модель коррелятора (Статистический эквивалент коррелятора)
6	09.10	Аппаратная реализация коррелятора (Принципы построения и структура коррелятора. Цифровой генератор гармонического сигнала и дальномерного кода.)
7	16.10	Следящие системы (Система слежения за фазой сигнала. Структурная схема ССФ, дискриминаторы, следящий фильтр. Система слежения за частотой. Структурная схема ССЧ, дискриминаторы, следящий фильтр. Система слежения за задержкой. Структурная схема ССЗ, дискриминаторы, следящий фильтр. Система слежения за задержкой с поддержкой от ФАП. Комплексный фильтр.)	GNSS Planning	КМ-2: Статистический эквивалент коррелятора
8	23.10	Оценка SNR, детекторы захвата, детекторы CC
9	29.10	Обнаружение сигнала. (Обнаружение сигнала. Алгоритмы, статистические характеристики обнаружения.)
10	30.10	Поиск сигнала (Поиск сигнала по частоте и задержке. Алгоритмы поиска, быстрый поиск сигнала. Блок быстрого поиска)
11	13.11	Символьная и оверлейная синхронизация	Исследование коррелятора АП СРНС с помощью имитационной модели	КМ-3: защита ЛР1
12	20.11	Демодуляция навигационных данных
13	27.11	Кадровая синхронизация, декодирование, парсинг
14	04.12	Формирование измерений, расчет положения спутника		КМ-4: защита ЛР2
15	11.12	Модель наблюдений псевдодальности. Вторичная обработка измерений. Одношаговый алгоритм решения навигационной задачи. Контроль целостности	Решение навигационной задачи по псевдодальномерным измерениям	КМ-5: защита ЛР3, ЛР4
16	18.12	Помехоустойчивость АП СРНС
17	25.12	Зачет

Журнал успеваемости.

Правила аттестации

Обязательным условием для получения допуска к экзамену является выполнение всех контрольных мероприятий: сдача двух контрольных и защита 4 лабораторных работ.

При написании отчетов следует опираться на правила оформления ГОСТ 7.32 (в части форматирования, оформления рисунков, таблиц, списков и т.д.).

Приемка осуществляется через репозиторий на github на базе проекта gnssrecbasics2020.

Демо модели

Прогноз выходного сигнала коррелятора

Производится обработка сигнала Gps L1 C/A, сформированного лабораторным имитатором сигналов, синхронизированным с приемником. Сигнал перенесен с помощью РЧБ NT1065 на промежуточную частоту 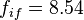$f_{if} = 8.54$ МГц и преобразован многоразрядным АЦП с частотой сэмплирования 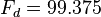$F_d = 99.375$ МГц. Установленная на имитаторе мощность обеспечивает уровень отношения сигнал/шум 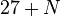$27 + N$ дБГц, где 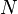$N$ - номер вариант по журналу.

В приемнике производтся корреляционная обработка сигнала, интервал накопления составляет 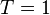$T = 1$ мс.

Сигнал имеет сдвиг частоты несущей 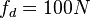$f_d = 100 N$ Гц, при этом опорный сигнал коррелятора имеет аналогичный сдвиг 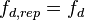$f_{d, rep} = f_d$. Задержка огибающей известна точно и используется в опорном сигнале $\tau = \tau_{rep}$.

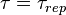Задание: Построить на плоскости I,Q вид множества точек корреляционных сумм, полученных в ходе большого (сотни) числа экспериментов.

Расчет выходного сигнала коррелятора  

clear all; clc; close all;

N = 30;

Fd = 99.375e6;
Td = 1/Fd;
T = 0.001;
fif = 8.34e6;

fd     = 100 * N;
fd_rep = fd;

phi     = 10 * N;
phi_rep = 20 * N;

qcno_dB = 27 + N;
qcno    = 10^(qcno_dB/10);

stdn = 50/3;
A    = sqrt(qcno * Td) * 2 * stdn; % qcno = A^2 / (4 stdn^2 Td)

fprintf('A = %f, stdn = %f\n', A, stdn);

L = fix(T * Fd);
t = (0:(L-1)) * Td;

PRN_Length = 1023;
PRN = (-1).^(rand(1, PRN_Length) > 0.5);

tau = 100500e-6;
tau_rep = tau;

nchip     = mod(fix(PRN_Length*(t - tau    )/T), PRN_Length) + 1;
nchip_rep = mod(fix(PRN_Length*(t - tau_rep)/T), PRN_Length) + 1;

Gc     = PRN(nchip    );
Gc_rep = PRN(nchip_rep);

So        = A * Gc     .* cos(2*pi*fif*t + 2*pi*fd    *t + deg2rad(phi)    );
S_rep_cos =     Gc_rep .* cos(2*pi*fif*t + 2*pi*fd_rep*t + deg2rad(phi_rep));
S_rep_sin =     Gc_rep .* sin(2*pi*fif*t + 2*pi*fd_rep*t + deg2rad(phi_rep));

K = 1000; I = nan(1, K); Q = nan(1,K);
for k = 1:K
    n = randn(1,L)*stdn;
 
    Gd     = (-1).^(rand(1,1) > 0.5);
    S = Gd * So;
   
    y = S + n;
   
    I(k) = y * S_rep_cos';
    Q(k) = y * S_rep_sin';
end

maxIQ = 1.1*max(abs(I + 1i*Q));

figure(1);
plot(t*1e3, [y; S; A*Gc]);
xlabel('t, ms')
ylabel('y, S');
grid on

figure(2);
plot(I, Q, '*')
hold on
plot([-maxIQ maxIQ], [0 0], 'k');
plot([0 0], [-maxIQ maxIQ], 'k');
quiver(-maxIQ, 0, 2*maxIQ, 0, 1, 'k');
quiver(0, -maxIQ, 0, 2*maxIQ, 1, 'k');
hold off
xlabel('I')
ylabel('Q');
axis equal
grid on

ЧАП и ФАП на стат эквивалентах

Слежение за фазой и частотой  

clear all; clc; close all;

T = 0.010;

Xist = [10;
         1];
     
Xfilt = [0;
         0];

Xfilt_FLL = [0;
             0];
     
F = [1 T;
     0 1];

Tmod = 10;
K = fix(Tmod / T);
 
G = [0;
     1];

std_ksi = 1.3 * T;
ksi = std_ksi * randn(1, K);

qcno_dB = 45;
qcno = 10^(qcno_dB/10);

stdnIQ = 7;
nI = stdnIQ * randn(1, K);
nQ = stdnIQ * randn(1, K);
A_IQ = sqrt(2*qcno*T) * stdnIQ;  

dF_PLL = 20;
Kfilt_PLL = [ 8/3 * dF_PLL   * T;
              32/9 * dF_PLL^2 * T];

dF_FLL = 3;
Kfilt_FLL = [ 8/3 * dF_FLL   * T;
              32/9 * dF_FLL^2 * T];
         
t = (1:K)*T;
phi_ist  = nan(1, K);
  w_ist  = nan(1, K);
phi_filt = nan(1, K);
  w_filt = nan(1, K);
phi_filt_FLL = nan(1, K);
  w_filt_FLL = nan(1, K);
 
phi_corr = 0; Iold = 0; Qold = 0;
for k = 1:K
    Xist = F * Xist + G * ksi(k);
   
    phi_ist(k) = Xist(1);
      w_ist(k) = Xist(2);
   
    % PLL
    Xfilt_extr = F*Xfilt;
    phi_extr = Xfilt_extr(1);
    dPhi = phi_ist(k) - phi_extr;

    Q = - A_IQ * sin(dPhi) + nQ(k);
    Ud = -Q;  
    Sd = A_IQ;  
   
    Xfilt = Xfilt_extr + Kfilt_PLL * Ud/Sd;

    phi_filt(k) = Xfilt(1);
      w_filt(k) = Xfilt(2);
   
    % FLL
    Xfilt_extr_FLL = F*Xfilt_FLL;
    w_extr = Xfilt_extr_FLL(1);
    dPhi = phi_ist(k) - phi_corr;
    phi_corr = phi_corr + w_extr * T;
    dW = w_ist(k) - w_extr;

    I = - A_IQ * cos(dPhi) + nI(k);
    Q = - A_IQ * sin(dPhi) + nQ(k);
    Ud = Q*Iold - I*Qold;  
    Sd = A_IQ;  
    Iold = I; Qold = Q;
   
    Xfilt_FLL = Xfilt_extr_FLL + Kfilt_FLL * Ud/Sd;

    phi_filt_FLL(k) = phi_corr;
      w_filt_FLL(k) = Xfilt_FLL(1);
   
   
end

figure(1)
subplot(2,1,1)
plot(t, phi_ist/2/pi, t, phi_filt/2/pi, t, phi_filt_FLL/2/pi)
ylabel('\phi, cycles')
subplot(2,1,2)
plot(t, rad2deg(w_ist), t, rad2deg(w_filt), t, rad2deg(w_filt_FLL))
ylabel('\omega, Hz')
xlabel('t, sec')

Вопросы к экзамену

Экзамен проводится в устной форме и содержит два вопроса (экзаменационные вопросы). При подготовке рекомендуется использовать книги по тематике, конспекты лекций и презентации.

Курсовая работа

Название: Разработка модуля расчёта координат спутника Beidou

Курсовая работа по АП СРНС выполняется во втором семестре. В рамках проекта студенты знакомятся с рядом инструментов и техник, используемых при разработке навигационных приемников.

Цель проекта - добавление в программное обеспечение приемника функции расчета положения спутника Beidou на заданное время по данным его эфемерид.

Требования к разрабатываемому программному модулю:

• требования назначения;
• отсутствие утечек памяти;
• малое время выполнения;
• низкий расход памяти;
• корректное выполнение при аномальных входных данных.

Для достижения цели выполняется ряд задач, соответствующих этапам проекта и контрольным мероприятиям:

• обработка данных от приемника, работа со сторонними сервисами для подготовки входных и проверочных данных для разрабатываемого модуля;
• моделирование модуля в Matlab/Python;
• реализация программного модуля на С/С++, включая юнит-тестирование в Check.

Этапы курсовой работы отличаются осваиваемыми инструментами.

На каждом из этапов действуют следующие правила:

• Взаимодействие осуществляется через github (пул реквесты, комментарии)
• Этап сдан тогда, когда принят пул реквест

Журнал с номерами спутников

Этап 1. Использование сторонних средств

Дедлайн: 03.03.21 (устранение замечаний и итоговый мёрдж до 09.03.21)

Конечная цель всего курсового проекта - получить библиотеку функций на Си++, позволяющую рассчитывать положение спутника Beidou по его эфемеридам. На первом этапе подготовим вспомогательные данные для разработки: эфемериды и оценки положения спутника от сторонних сервисов (чтобы было с чем сравниваться на след. этапах)

На крыше корпуса Е МЭИ установлена трехдиапазонная антенна Harxon HX-CSX601A. Она через 50-метровый кабель, сплиттер, bias-tee и усилитель подключена к трем навигационным приемникам:

• Javad Lexon LGDD,
• SwiftNavigation Piksi Multi,
• Clonicus разработки ЛНС МЭИ.

Эти приемники осуществляют первичную обработку сигналов Beidou B1I, выдавая по интерфейсам соответствующие потоки данных - наблюдения псевдодальностей и эфемериды спутников. Данные от приемника Clonicus, записанные вечером 16 февраля 2021 года, доступны в рабочем репозитории (директория logs) в нескольких форматах.

Во-первых, это дамп бинарного потока данных от приемника в формате NVS BINR.

Во-вторых, текстовый файл данных пакета 0xF7, полученный из данного дампа - для тех, кому лень разбираться с бинарным файлом и протоколом. Он получен подобным printf'ом для каждого спутника с периодом передачи эфемерид:

fprintf(fid, "%2u %9.3f %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %22.17e %u %u %u %u %u %u\n",
        pack->SatNum,       // 1
        pack->bds[0].toe,   // 2
        pack->bds[0].Crs,   // 3
        pack->bds[0].Dn,    // 4
        pack->bds[0].M0,    // 5
        pack->bds[0].Cuc,   // 6
        pack->bds[0].e,     // 7
        pack->bds[0].Cus,   // 8
        pack->bds[0].sqrtA, // 9
        pack->bds[0].Cic,   // 10
        pack->bds[0].Omega0,// 11
        pack->bds[0].Cis,   // 12
        pack->bds[0].i0,    // 13
        pack->bds[0].Crc,   // 14
        pack->bds[0].omega, // 15
        pack->bds[0].OmegaDot, // 16
        pack->bds[0].iDot,  // 17
        pack->bds[0].Tgd,   // 18
        pack->bds[0].toc,   // 19
        pack->bds[0].af2,   // 20
        pack->bds[0].af1,   // 21
        pack->bds[0].af0,   // 22
        pack->bds[0].URA,   // 23
        pack->bds[0].IODE,  // 24
        pack->bds[0].IODC,  // 25
        pack->bds[0].codeL2,// 26
        pack->bds[0].L2P,   // 27
        pack->bds[0].WN     // 28
        );

Для приемки первого этапа оформляется отчет по ГОСТ 7.32, содержащий результаты работ:

1. Определение формы орбиты и положения спутника на ней на начало рассматриваемого интервала времени по данным сервиса CelesTrak: общий вид + положение спутника на 18:00 МСК 16 февраля 2021, так, чтобы было видно подспутниковую точку и время (примерно так)
2. Расчет графика угла места собственного спутника от времени по данным Trimble GNSS Planning Online на интервал времени с 18:00 МСК 16 февраля до 06:00 МСК 17 февраля 2021 года.
3. Расчет диаграммы угла места и азимута спутника (SkyView, он же SkyPlot) по данным Trimble GNSS Planning Online на на интервал времени с 18:00 МСК 16 февраля до 06:00 МСК 17 февраля 2021 года.
4. Формирование списка и описание параметров, входящих в состав эфемерид в сигнале B1I Beidou
5. Формирование таблицы эфемерид собственного спутника (номер спутника Beidou см. в журнале выше) с подписанными размерностями (как тут, но только для одного спутника)

Работа осуществляется в репозитории на github на базе bdsephexercise. Для этого:

1. Завести, если до сих пор нет, аккаунт на github
2. Сделать форк проекта bdsephexercise (маленькая кнопка сверху справа в вэб-интерфейсе)
3. Установить на рабочем компьютере git (для выполнения последующих этапов удобнее будет сделать это в ОС GNU/Linux, вероятно, на виртуальной машине)
4. Клонировать свой форк на рабочий компьютер (git clone https://github.com/MySuperAccount/bdsephexercise.git)
5. Промежуточные и итоговые результаты по первому этапу хранить в каталоге processing (git pull; git add <files>; git commit -m "Сделал то-то то-то"; git push)
6. По результатам первого этапа завести Pull Request в исходный проект в ветку, название которой совпадает с вашей фамилией (кнопка наверху в вэб-интерфейсе)
7. Устранить все замечания, добиться принятия Pull Request'а.

Этап сдан тогда, когда ваш ПР принят.

Этап 2. Моделирование

Дедлайн: 02.04.21 (исправления замечаний до 09.04.21)

Эфемериды - параметры некоторой модели движения спутника. В разных ГНСС эти модели разные, а значит отличается и формат эфемерид, и алгоритмы расчета положения спутника.

Одна из самых простых и удобных моделей - в системе GPS. Beidou наследует данную модель.

Требуется реализовать на языке Matlab или Python функцию расчета положения спутника Beidou на заданный момент по шкале времени UTC. В качестве эфемерид использовать данные, полученные на предыдущем этапе.

Построить трехмерные графики множества положений спутника Beidou с системным номером, соответствующим номеру студента по списку. Графики в двух вариантах: в СК ECEF WGS84 и соответствующей ей инерциальной СК. Положения должны соответствовать временному интервалу с 18:00 МСК 16 февраля до 06:00 МСК 17 февраля 2021 года. Допускается использовать одни и те же эфемериды на весь рассматриваемый интервал.

Построить SkyView за указанный временной интервал (напоминаю, антенна на крыше корпуса Е) и сравнить результат с Trimble GNSS Planning Online, полученный на прошлом этапе.

Оформить отчет по результатам этапа:

1. Реализация в Matlab или Python (описание модели и её листинг)
2. Таблица использованных эфемерид
3. Трехмерные графики положений спутника в ECEF и ECI (не забудьте подписать оси, изобразите соответствующую Земле сферу в начале СК)
4. Расчётный и полученный в GNSS Planing Online SkyView
5. Сравнение результатов моделирования с результатами первого этапа

Работы по данному этапу осуществляются в каталоге simulation. Правила приемки этапа те же, что и на первом этапе.

Этап 3. Реализация

Дедлайн: 11.05.21 (исправления до 18.05.21)

Требуется разработать на языке С/С++ функцию расчета положения спутника Beidou на заданное время по шкале UTC, минимизируя время её исполнения и количество затрачиваемой оперативной памяти. Вызов функции не должен приводить к выбросу исключений или утечкам памяти при любом наборе входных данных.

Функция расчета положения спутника в Matlab/Python относительно проста, т.к. доступны библиотеки линейной алгебры и решения уравнений. Но при разработке встраиваемого ПО приходится сохранять лицензионную частоту, минимизировать вычислительную нагрузку и затраты памяти. Поэтому отобразить модель из Matlab/Python в прошивку приемника дословно, как правило, не получается. В рассматриваемом примере потребуется, как минимум, выполнить свою реализацию решения трансцендентного уравнения.

Программный модуль должен сопровождаться unit-тестами под check:

• Тесты функции решения уравнения Кеплера
• Тест расчетного положения спутника в сравнении с Matlab/Python с шагом 0.1 секунды.

Во время второго теста должно вычисляться и выводиться средняя длительность исполнения функции. Допускается использовать одни и те же эфемериды на весь рассматриваемый интервал (как на предыдущем этапе).

Требуется провести проверку на утечки памяти с помощью утилиты valgrind.

Оформить отчет по результатам курсового проекта. В качестве первых двух глав использовать отчёты с предыдущих этапов, в третьей главе отразить результаты этого этапа:

1. Код реализации
2. Вывод тестов, включая анализ времени исполнения
3. Вывод valgrind
4. Вывод по этапу
5. Заключение по проекту

В репозитории расположен каркас программного модуля libbdssvpos, представленного в виде подключаемой библиотеки на базе системы сборки CMake. Настроена компиляция статической/динамической библиотек компилятором/кросскомпилятором и выполнение юнит-тестов (проверено в GNU/Linux системах). Для примера в библиотеке реализованы две функции: умножения и сложения.

В функцию сложения add внесена ошибка, на которую указывает результат соответствующего юнит-теста:

korogodin@KorPC:~/bdsephexercise/libbdssvpos$ mkdir build
korogodin@KorPC:~/bdsephexercise/libbdssvpos$ cd build
korogodin@KorPC:~/bdsephexercise/libbdssvpos/build$ cmake ..
-- The C compiler identification is GNU 5.4.0
-- The CXX compiler identification is GNU 5.4.0
-- Check for working C compiler: /usr/bin/cc
-- Check for working C compiler: /usr/bin/cc -- works
-- Detecting C compiler ABI info
-- Detecting C compiler ABI info - done
-- Detecting C compile features
-- Detecting C compile features - done
-- Check for working CXX compiler: /usr/bin/c++
-- Check for working CXX compiler: /usr/bin/c++ -- works
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-- libbdssvpos version: cd76a7e
-- Found PkgConfig: /usr/bin/pkg-config (found version "0.29.1")
-- Checking for one of the modules 'check'
-- Configuring done
-- Generating done
-- Build files have been written to: /home/korogodin/bdsephexercise/libbdssvpos/build
korogodin@KorPC:~/bdsephexercise/libbdssvpos/build$ make
[ 33%] Built target bdssvpos-static
[ 66%] Built target bdssvpos
Scanning dependencies of target test_bdssvpos
[ 77%] Building CXX object test/CMakeFiles/test_bdssvpos.dir/check_position.cpp.o
[ 88%] Linking CXX executable test_bdssvpos
Running unit tests
Running suite(s): My test suite
50%: Checks: 2, Failures: 1, Errors: 0
/home/korogodin/bdsephexercise/libbdssvpos/test/check_position.cpp:11:F:Main tests:test_add:0: 1+2 should be 3
test/CMakeFiles/test_bdssvpos.dir/build.make:121: ошибка выполнения рецепта для цели «test/test_bdssvpos»
make[2]: *** [test/test_bdssvpos] Ошибка 1
make[2]: *** Удаляется файл «test/test_bdssvpos»
CMakeFiles/Makefile2:179: ошибка выполнения рецепта для цели «test/CMakeFiles/test_bdssvpos.dir/all»
make[1]: *** [test/CMakeFiles/test_bdssvpos.dir/all] Ошибка 2
Makefile:127: ошибка выполнения рецепта для цели «all»
make: *** [all] Ошибка 2

Работы по данному этапу осуществляются в каталоге libbdssvpos. Правила приемки этапа те же.

Курсовая прошлых лет

А в 2019 году задание выглядело так.