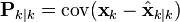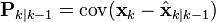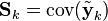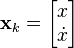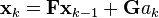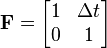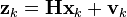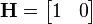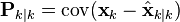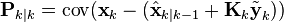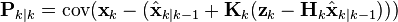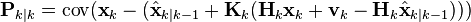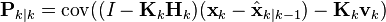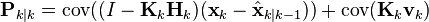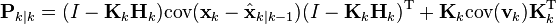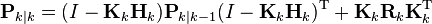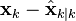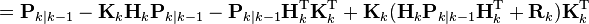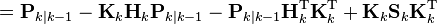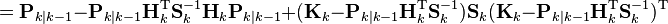Фильтр Калмана

|
|
Фи́льтр Ка́лмана — эффективный рекурсивный фильтр, оценивающий вектор состояния динамической системы, используя ряд неполных и зашумленных измерений. Назван в честь Рудольфа Калмана.
Фильтр Калмана широко используется в инженерных и эконометрических приложениях: от радаров и систем технического зрения до оценок параметров макроэкономических моделей[1][2]. Калмановская фильтрация является важной частью теории управления, играет большую роль в создании систем управления. Совместно с линейно-квадратичным регулятором фильтр Калмана позволяет решить задачу линейно-квадратичного гауссовского управления. Фильтр Калмана и линейно-квадратичный регулятор — возможное решение большинства фундаментальных задач в теории управления.
В большинстве приложений количество параметров, задающих состояние объекта, больше, чем количество наблюдаемых параметров, доступных для измерения. При помощи модели объекта по ряду доступных измерений фильтр Калмана позволяет получить оценку внутреннего состояния.
Фильтр Калмана предназначен для рекурсивного дооценивания вектора состояния априорно известной динамической системы, то есть для расчёта текущего состояния системы необходимо знать текущее измерение, а также предыдущее состояние самого фильтра. Таким образом, фильтр Калмана, как и множество других рекурсивных фильтров, реализован во временно́м, а не в частотном представлении.
Наглядный пример возможностей фильтра — получение точных, непрерывно обновляемых оценок положения и скорости некоторого объекта по результатам временно́го ряда неточных измерений его местоположения. Например, в радиолокации стоит задача сопровождения цели, определения её местоположения, скорости и ускорения, при этом результаты измерений поступают постепенно и сильно зашумлены. Фильтр Калмана использует вероятностную модель динамики цели, задающую тип вероятного движения объекта, что позволяет снизить воздействие шума и получить хорошие оценки положения объекта в настоящий, будущий или прошедший момент времени.
Содержание |
Введение
Фильтр Калмана оперирует понятием вектора состояния системы (набором параметров, описывающих состояние системы на некоторый момент времени) и его статистическим описанием. В общем случае динамика некоторого вектора состояния описывается плотностями вероятности распределения его компонент в каждый момент времени. При наличии определенной математической модели производимых наблюдений за системой, а также модели априорного изменения параметров вектора состояния (а именно — в качестве марковского формирующего процесса) можно записать уравнение для апостериорной плотности вероятности вектора состояния в любой момент времени. Данное дифференциальное уравнение носит название уравнение Стратоновича. Уравнение Стратоновича в общем виде не решается. Аналитическое решение удается получить только в случае ряда ограничений (предположений):
- гауссовости априорных и апостериорных плотностей вероятности вектора состояния на любой момент времени (в том числе начальный)
- гауссовости формирующих шумов
- гауссовости шумов наблюдений
- белости шумов наблюдений
- линейности модели наблюдений
- линейности модели формирующего процесса (который, напомним, должен являться марковским процессом)
Классический фильтр Калмана является уравнениями для расчета первого и второго момента апостериорной плотности вероятности (в смысле вектора математических ожиданий и матрицы дисперсий, в том числе взаимных) при данных ограничениях. Ввиду того, что для нормальной плотности вероятности математическое ожидание и дисперсионная матрица полностью задают плотность вероятности, можно сказать, что фильтр Калмана рассчитывает апостериорную плотность вероятности вектора состояния на каждый момент времени. А значит полностью описывает вектор состояния как случайную векторную величину.
Расчетные значения математических ожиданий при этом являются оптимальными оценками по критерию среднеквадратической ошибки, что и обуславливает его широкое применение.
Существует несколько разновидностей фильтра Калмана, отличающихся приближениями и ухищрениями, которые приходится применять для сведения фильтра к описанному виду и уменьшения его размерности:
- Расширенный фильтр Калмана (EKF, Extended Kalman filter). Сведение нелинейных моделей наблюдений и формирующего процесса с помощью линеаризации посредством разложения в ряд Тейлора.
- Unscented Kalman filter (UKF). Используется в задачах, в которых простая линеаризация приводит к уничтожению полезных связей между компонентами вектора состояния. В этом случае «линеаризация» основана на unscented-преобразовании.
- Ensemble Kalman filter (EnKF). Используется для уменьшения размерности задачи.
- Возможны варианты с нелинейным дополнительным фильтром, позволяющим привести негауссовские наблюдения к нормальным.
- Возможны варианты с «обеляющим» фильтром, позволяющим работать с «цветными» шумами
- и т. д.
Используемая модель динамической системы
Фильтры Калмана базируются на дискретизированных по времени линейных динамических системах. Такие системы моделируются цепями Маркова при помощи линейных операторов и слагаемых с нормальным распределением. Состояние системы описывается вектором конечной размерности — вектором состояния. В каждый такт времени линейный оператор действует на вектор состояния и переводит его в другой вектор состояния (детерминированное изменение состояния), добавляется некоторый вектор нормального шума (случайные факторы) и в общем случае вектор управления, моделирующий воздействие системы управления. Фильтр Калмана можно рассматривать как аналог скрытым моделям Маркова, с тем отличием, что переменные, описывающие состояние системы, являются элементами бесконечного множества действительных чисел (в отличие от конечного множества пространства состояний в скрытых моделях Маркова). Кроме того, скрытые модели Маркова могут использовать произвольные распределения для последующих значений вектора состояния, в отличие от фильтра Калмана, использующего модель нормально распределенного шума. Существует строгая взаимосвязь между уравнениями фильтра Калмана и скрытой модели Маркова. Обзор этих и других моделей дан Roweis и Chahramani (1999)[3].
При использовании фильтра Калмана для получения оценок вектора состояния процесса по серии зашумленных измерений необходимо представить модель данного процесса в соответствии со структурой фильтра — в виде матричного уравнения определенного типа. Для каждого такта k работы фильтра необходимо в соответствии с приведенным ниже описанием определить матрицы: эволюции процесса Fk; матрицу наблюдений Hk; ковариационную матрицу процесса Qk; ковариационную матрицу шума измерений Rk; при наличии управляющих воздействий — матрицу их коэффициентов Bk.
Модель системы/процесса подразумевает, что истинное состояние в момент k получается из истинного состояния в момент k−1 в соответствии с уравнением:
-
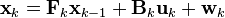 ,
,
где
- Fk — матрица эволюции процесса/системы, которая воздействует на вектор xk−1 (вектор состояния в момент k−1);
- Bk — матрица управления, которая прикладывается к вектору управляющих воздействий uk;
- wk — нормальный случайный процесс с нулевым математическим ожиданием и ковариационной матрицей Qk, который описывает случайный характер эволюции системы/процесса:
В момент k производится наблюдение (измерение) zk истинного вектора состояния xk, которые связаны между собой уравнением:
где Hk — матрица измерений, связывающая истинный вектор состояния и вектор произведенных измерений, vk — белый гауссовский шум измерений с нулевым математическим ожиданием и ковариационной матрицей Rk:
Начальное состояние и векторы случайных процессов на каждом такте {x0, w1, …, wk, v1, …, vk} считаются независимыми.
Многие реальные динамические системы нельзя точно описать данной моделью. На практике неучтённая в модели динамика может серьёзно испортить рабочие характеристики фильтра, особенно при работе с неизвестным стохастическим сигналом на входе. Более того, неучтённая в модели динамика может сделать фильтр неустойчивым. С другой стороны, независимый белый шум в качестве сигнала не будет приводить к расхождению алгоритма. Задача отделения шумов измерений от неучтенной в модели динамики сложна, решается она с помощью теории робастных систем управления.
Фильтр Калмана
Фильтр Калмана является разновидностью рекурсивных фильтров. Для вычисления оценки состояния системы на текущий такт работы ему необходима оценка состояния (в виде оценки состояния системы и оценки погрешности определения этого состояния) на предыдущем такте работы и измерения на текущем такте. Данное свойство отличает его от пакетных фильтров, требующих в текущий такт работы знание истории измерений и/или оценок. Далее под записью 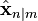 будем понимать оценку истинного вектора
будем понимать оценку истинного вектора 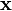 в момент n с учетом измерений с момента начала работы и по момент m включительно.
в момент n с учетом измерений с момента начала работы и по момент m включительно.
Состояние фильтра задается двумя переменными:
-
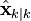 — апостериорная оценка состояния объекта в момент k полученная по результатам наблюдений вплоть до момента k включительно (в русскоязычной литературе часто обозначается
— апостериорная оценка состояния объекта в момент k полученная по результатам наблюдений вплоть до момента k включительно (в русскоязычной литературе часто обозначается 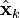 , где
, где  означает «оценка», а k — номер такта, на котором она получена);
означает «оценка», а k — номер такта, на котором она получена);
-
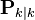 — апостериорная ковариационная матрица ошибок, задающая оценку точности полученной оценки вектора состояния и включающая в себя оценку дисперсий погрешности вычисленного состояния и ковариации, показывающие выявленные взаимосвязи между параметрами состояния системы (в русскоязычной литературе часто обозначается
— апостериорная ковариационная матрица ошибок, задающая оценку точности полученной оценки вектора состояния и включающая в себя оценку дисперсий погрешности вычисленного состояния и ковариации, показывающие выявленные взаимосвязи между параметрами состояния системы (в русскоязычной литературе часто обозначается 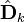 ).
).
Итерации фильтра Калмана делятся на две фазы: экстраполяция и коррекция. Во время экстраполяции фильтр получает предварительную оценку состояния системы  (в русскоязычной литературе часто обозначается
(в русскоязычной литературе часто обозначается 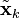 , где
, где  означает «экстраполяция», а k — номер такта, на котором она получена) на текущий шаг по итоговой оценке состояния с предыдущего шага (либо предварительную оценку на следующий такт по итоговой оценке текущего шага, в зависимости от интерпретации). Эту предварительную оценку также называют априорной оценкой состояния, так как для её получения не используются наблюдения соответствующего шага. В фазе коррекции априорная экстраполяция дополняется соответствующими текущими измерениями для коррекции оценки. Скорректированная оценка также называется апостериорной оценкой состояния, либо просто оценкой вектора состояния
означает «экстраполяция», а k — номер такта, на котором она получена) на текущий шаг по итоговой оценке состояния с предыдущего шага (либо предварительную оценку на следующий такт по итоговой оценке текущего шага, в зависимости от интерпретации). Эту предварительную оценку также называют априорной оценкой состояния, так как для её получения не используются наблюдения соответствующего шага. В фазе коррекции априорная экстраполяция дополняется соответствующими текущими измерениями для коррекции оценки. Скорректированная оценка также называется апостериорной оценкой состояния, либо просто оценкой вектора состояния 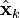 .
Обычно эти две фазы чередуются: экстраполяция производится по результатам коррекции до следующего наблюдения, а коррекция производится совместно с доступными на следующем шаге наблюдениями, и т. д. Однако возможно и другое развитие событий, если по некоторой причине наблюдение оказалось недоступным, то этап коррекции может быть пропущен и выполнена экстраполяция по нескорректированной оценке (априорной экстраполяции). Аналогично, если независимые измерения доступны только в отдельные такты работы, всё равно возможны коррекции (обычно с использованием другой матрицы наблюдений Hk).
.
Обычно эти две фазы чередуются: экстраполяция производится по результатам коррекции до следующего наблюдения, а коррекция производится совместно с доступными на следующем шаге наблюдениями, и т. д. Однако возможно и другое развитие событий, если по некоторой причине наблюдение оказалось недоступным, то этап коррекции может быть пропущен и выполнена экстраполяция по нескорректированной оценке (априорной экстраполяции). Аналогично, если независимые измерения доступны только в отдельные такты работы, всё равно возможны коррекции (обычно с использованием другой матрицы наблюдений Hk).
Далее рассмотрим работу классического оптимального фильтра Калмана.
Этап экстраполяции
| Экстраполяция (предсказание) вектора состояния системы по оценке вектора состояния и примененному вектору управления с шага (k−1) на шаг k: | 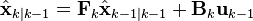
|
| Ковариационная матрица для экстраполированного вектора состояния: | 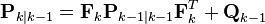
|
Этап коррекции
| Отклонение полученного на шаге k наблюдения от наблюдения, ожидаемого при произведенной экстраполяции: | 
|
| Ковариационная матрица для вектора отклонения (вектора ошибки): | 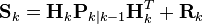
|
| Оптимальная по Калману матрица коэффициентов усиления, формирующаяся на основании ковариационных матриц имеющейся экстраполяции вектора состояния и полученных измерений (посредством ковариационной матрицы вектора отклонения): | 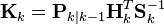
|
| Коррекция ранее полученной экстраполяции вектора состояния — получение оценки вектора состояния системы: | 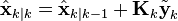
|
| Расчет ковариационной матрицы оценки вектора состояния системы: | 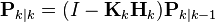
|
Выражение для ковариационной матрицы оценки вектора состояния системы справедливо только при использовании приведенного оптимального вектора коэффициентов. В общем случае это выражение имеет более сложный вид.
Инварианты
Если модель абсолютно точна и абсолютно точно заданы начальные условия  и
и 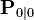 , то следующие величины сохраняются после любого количества итераций работы фильтра — являются инвариантами:
, то следующие величины сохраняются после любого количества итераций работы фильтра — являются инвариантами:
Математические ожидания оценок и экстраполяций вектора состояния системы, матрицы ошибок являются нуль-векторами:
где ![\textsf{E}[\xi]](/images/math/0/d/3/0d3cc0edc5c6832ffee41c46a40b0d8a.png) — математическое ожидание
— математическое ожидание 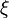 .
.
Расчетные матрицы ковариаций экстраполяций, оценок состояния системы и вектора ошибок совпадают с истинными матрицами ковариаций:
Пример построения фильтра
Представим себе вагонетку, стоящую на бесконечно длинных рельсах при отсутствующем трении. Изначально она покоится в позиции 0, но под действием случайных факторов на неё действует случайное ускорение. Мы измеряем положение вагонетки каждые ∆t секунд, но измерения неточны. Мы хотим получать оценки положения вагонетки и её скорости. Применим к этой задаче фильтр Калмана, определим все необходимые матрицы.
В данной задаче матрицы F, H, R и Q не зависят от времени, опустим их индексы. Кроме того, мы не управляем вагонеткой, поэтому матрица управления B отсутствует.
Координата и скорость вагонетки описывается вектором в линейном пространстве состояний
где 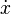 — скорость (первая производная координаты
— скорость (первая производная координаты 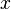 по времени).
по времени).
Будем считать, что между (k−1)-ым и k-ым тактами вагонетка движется с постоянным ускорением ak, распределенным по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением σa. В соответствии с механикой Ньютона можно записать
где
и
-
 .
.
Ковариационная матрица случайных воздействий
-
![\textbf{Q} = \textrm{cov}(\textbf{G}a) = \textsf{E}[(\textbf{G}a)(\textbf{G}a)^{\text{T}}] = \textbf{G} \textsf{E}[a^2] \textbf{G}^{\text{T}} = \textbf{G}[\sigma_a^2]\textbf{G}^{\text{T}} = \sigma_a^2 \textbf{G}\textbf{G}^{\text{T}}](/images/math/a/a/b/aab49f3237e597fff0639550c1acc944.png) (σa — скаляр).
(σa — скаляр).
На каждом такте работы производится измерение положения вагонетки. Предположим, что погрешность измерений vk имеет нормальное распределение с нулевым математическим ожиданием и среднеквадратическим отклонением σz. Тогда
где
и ковариационная матрица шума наблюдений имеет вид
-
![\textbf{R} = \textsf{E}[\textbf{v}_k \textbf{v}_k^{\text{T}}] = \begin{bmatrix} \sigma_z^2 \end{bmatrix}](/images/math/a/e/6/ae65d18cba7ca0de206897780238d51a.png) .
.
Начальное положение вагонетки известно точно
-
 ,
,
-
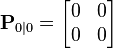 .
.
Если же положение и скорость вагонетки известна лишь приблизительно, то можно инициализировать матрицу дисперсий достаточно большим числом L, чтобы при этом число превосходило дисперсию измерений координаты
-
 ,
,
-
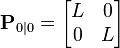 .
.
В этом случае на первых тактах работы фильтр будет с бо́льшим весом использовать результаты измерений, чем имеющуюся априорную информацию.
Вывод формул
Ковариационная матрица оценки вектора состояния
По определению ковариационной матрицы Pk|k
подставляем выражение для оценки вектора состояния 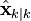
и расписываем выражение для вектора ошибок 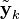
и вектора измерений 
выносим вектор погрешности измерений vk
так как вектор погрешности измерений vk не коррелирован с другими аргументами, получаем выражение
в соответствии со свойствами ковариации векторов данное выражение преобразуется к виду
заменяя выражение для ковариационной матрицы экстраполяции вектора состояния на Pk|k−1 и определение ковариационной матрицы шумов наблюдений на Rk, получаем
Полученное выражение справедливо для произвольной матрицы коэффициентов, но если в качестве неё выступает матрица коэффициентов, оптимальная по Калману, то данное выражение для ковариационной матрицы можно упростить.
Оптимальная матрица коэффициентов усиления
Фильтр Калмана минимизирует сумму квадратов математических ожиданий ошибок оценки вектора состояния.
Вектор ошибки оценки вектора состояния
Стоит задача минимизировать сумму математических ожиданий квадратов компонент данного вектора
-
![\textsf{E}[\;|\textbf{x}_{k} - \hat{\textbf{x}}_{k|k}|^2\,]](/images/math/4/e/d/4ede0ed1a8517ecd1dcd1a4b0108986d.png) ,
,
что эквивалентно минимизации следа ковариационной матрицы оценки вектора состояния Pk|k. Подставим в выражение для ковариационной матрицы оценки вектора состояния имеющиеся выражения и дополним до полного квадрата:
Заметим что, последнее слагаемое является ковариационной матрицей некоторой случайной величины, поэтому его след неотрицателен. Минимум следа достигнется при обнулении последнего слагаемого:
Утверждается, что данная матрица является искомой и при использовании в качестве матрицы коэффициентов в фильтре Калмана минимизирует сумму средних квадратов ошибок оценки вектора состояния.
Ковариационная матрица оценки вектора состояния при использовании оптимальной матрицы коэффициентов
Выражение для ковариационной матрицы оценки вектора состояния Pk|k при использовании оптимальной матрицы коэффициентов примет вид:
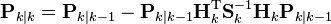
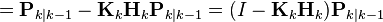 .
.
Данная формула вычислительно проще и поэтому практически всегда используется на практике, но она корректна только при использовании оптимальной матрицы коэффициентов. Если ввиду малой вычислительной точности возникает проблема с вычислительной устойчивостью, либо специально используется матрица коэффициентов, отличная от оптимальной, следует использовать общую формулу для ковариационной матрицы оценки вектора состояния.
Критика фильтра Калмана
На настоящий момент основная критика фильтра Калмана ведётся по следующим направлениям[4]:
- В фильтре Калмана погрешности представлены белым шумом, которого на самом деле в природе не существует.
- Нет соответствия необходимому и достаточному условию оптимальности
-
![\textsf{M}[\varepsilon(t)\,\textbf{Z}_{k}]^\text{T} = 0](/images/math/5/b/7/5b723037ff2c0391351b7f0a2b79a0f7.png) при
при 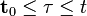
- Ошибка в выводе фильтра Калмана — требуются противоречивые условия верности разных уравнений алгоритма: в одних чтобы τ < t и в других τ = t.
Соответственно, позиция сторонников оптимальности данного фильтра заключается в том, что[5]:
- Возможно составить модифицированый фильтр Калмана, у которого погрешности будут представлены цветным шумом.
- Использование условия оптимальности
![\textsf{M}[\varepsilon(t)\,\textbf{Z}_{k}]^\text{T} = 0\quad](/images/math/6/f/b/6fb24f8996ab8dce739081fc81b272cc.png) в определённых случаях приводит к менее точному результату, нежели используемое в фильтре Калмана.
в определённых случаях приводит к менее точному результату, нежели используемое в фильтре Калмана.
- При выводе фильтра Калмана можно принять условия: τ < t, τ → t. Принятие их устраняет противоречие.
Где используется
- Курсовертикали
- Автопилот
- Навигационные системы:
- Инерциальные
- Рельефометрические (по цифровым картам местности)
- Спутниковые
Литература и публикации
- Перевод статьи «Kalman Filter»
- «Фильтр Калмана для „чайников“: матрица наблюдаемости и фундаментальная матрица»
- Peter Joseph «INTRODUCTORY LESSON: The one-dimensional Kalman Filter»
- Николай Некипелов «Калмановская фильтрация»
- Перов, А. И. Статистическая теория радиотехнических систем. — М.: Радиотехника, 2003. — 400 с. — ISBN 5-93108-047-3
Примечания
- ↑ Шаблон:Citation
- ↑ Шаблон:Citation
- ↑ Roweis, S. and Ghahramani, Z., A unifying review of linear Gaussian models, Neural Comput. Vol. 11, No. 2, (February 1999), pp. 305—345.
- ↑ http://www.tgizd.ru/mag/aviakos/aviakos_7_6_7.shtml Г. Ф. Савинов О некоторых особенностях алгоритма оптимальной фильтрации Калмана — Бьюси // Авиакосмическое приборостроение № 6, 2007 г.
- ↑ http://www.tgizd.ru/mag/aviakos/aviakos_8_6_5.shtml А. Ю. Горбачев Критерии оценки алгоритмов оптимальной фильтрации // Авиакосмическое приборостроение № 6, 2008 г.
Шаблон:Math-stubar:مرشح كالمان ca:Filtre de Kalman de:Kalman-Filter en:Kalman filter eo:Filtrilo de Kalman es:Filtro de Kalman et:Kalmani filter fa:فیلتر کالمن fi:Kalman-suodin fr:Filtre de Kalman it:Filtro di Kalman ja:カルマンフィルター ko:칼만 필터 lt:Kalmano filtras nl:Kalman-filter pl:Filtr Kalmana pt:Filtro de Kalman sv:Kalmanfilter tr:Kalman Filtresi uk:Фільтр Калмана zh:卡尔曼滤波
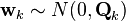
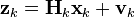

![\textsf{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k}] = \textsf{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}] = 0](/images/math/0/3/6/036bee1e2b0efd88a6ecb1d4dd18e0dd.png)
![\textsf{E}[\tilde{\textbf{y}}_k] = 0](/images/math/6/1/a/61a46df24b81624672b46445644d803b.png)