28.06.2011, Оптимальный прием сигнала в угломере в условиях многолучевости
Содержание |
Синтез алгоритмов
Проведен Александром Ивановичем. Получены алгоритмы дискриминаторов: первой разности фаз для прямого и отраженного фронтов, разности хода лучей.
Затем аналогичный синтез провел Корогодин И.В., взяв за модель наблюдений стат.эквиваленты корреляционных сумм. Результаты практически совпадают.
Моделирование
Пишется модель: Модель многолучевого распространения сигналов для угломера.
Алгоритм без компенсации ошибки многолучевости
Характерное поведение ошибки оценки первой разности фаз при наличии переотраженного сигнала при использовании простого дискриминатора разности фаз, синтезированного в отсутствии отраженного сигнала:
Ошибка напоминает биения - результат действия двух ошибок, вносимых многолучевостью в фазу - в первой и второй точке.
Синтезированный алгоритм при отсутствии ошибок по смежным параметрам
Использование нового дискриминатора при известных 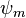 ,
, 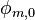 ,
, 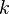 дает отличные результаты (
дает отличные результаты (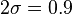 град., что совпадает с погрешностью в случае отсутствия многолучевости (SNR 45 дБГц, полоса СС 1 Гц)):
град., что совпадает с погрешностью в случае отсутствия многолучевости (SNR 45 дБГц, полоса СС 1 Гц)):
Данный результат можно интерпретировать как потенциальную точность слежения: ошибки по остальным направлениям пространства состояния равны нулю, погрешность определяется информацией Фишера и полосой фильтра. Точность порядка единицы градуса.
Синтезированный алгоритм: три связанных следящих системы
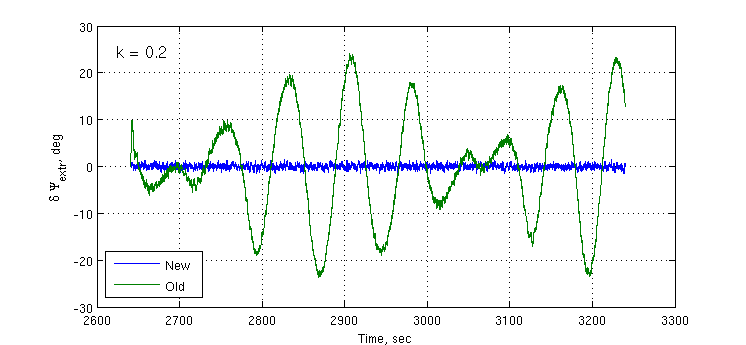
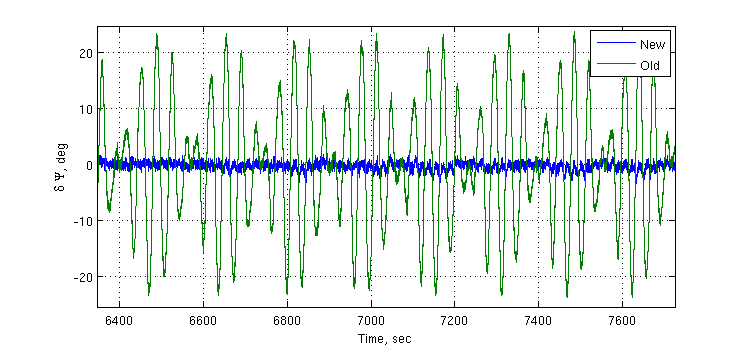
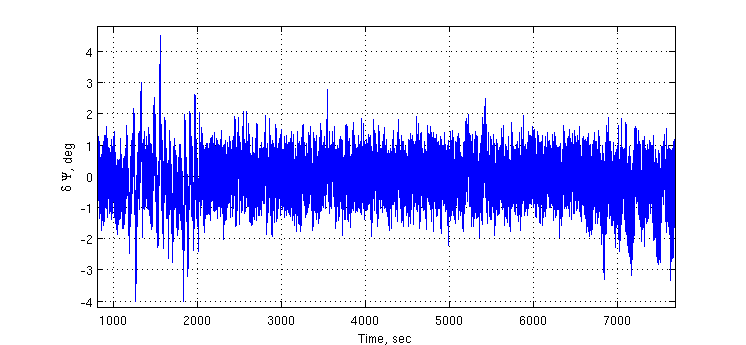
При совместной работе трех синтезированных СС погрешность определения первой разности фаз увеличивается примерно в полтора раза. Полосы СС: 1 Гц для 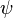 , 0.05 Гц для
, 0.05 Гц для 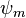 , 0.2 Гц для
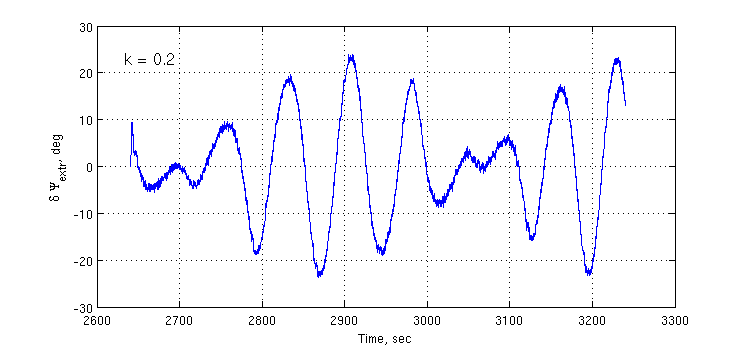
, 0.2 Гц для 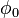 . Точность слежения за первой разностью фаз составила примерно 1.3 градуса против 23 градусов при использовании алгоритма без компенсации ошибок многолучевости и 0.9 градуса при отсутствии многолучевости. Параметр k = 0.2.
. Точность слежения за первой разностью фаз составила примерно 1.3 градуса против 23 градусов при использовании алгоритма без компенсации ошибок многолучевости и 0.9 градуса при отсутствии многолучевости. Параметр k = 0.2.
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.