Моделирование коррелированных гауссовых СВ — различия между версиями
Korogodin (обсуждение | вклад) |
Korogodin (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
Рассмотрим решение данной задачи на примере модели шумов статистического эквивалента корреляционных сумм <math>I_p</math>, <math>I_e</math> и <math>I_l</math>. | Рассмотрим решение данной задачи на примере модели шумов статистического эквивалента корреляционных сумм <math>I_p</math>, <math>I_e</math> и <math>I_l</math>. | ||
| + | |||
| + | == Статистический эквивалент коррелятора == | ||
| + | |||
| + | Статистический эквивалент коррелятора синфазных корреляционных сумм можно описать рядом выражений: | ||
| + | |||
| + | <math>I_p = A_{IQ} \rho\left(\delta \tau\right) sinc\left(\frac{\delta \omega T}{2}\right) cos\left(\frac {\delta \omega T}{2} + \delta\varphi\right) + n_{Ip}</math> | ||
| + | |||
| + | <math>I_{e} = A_{IQ} \rho\left(\delta \tau - \frac{\Delta \tau}{2}\right) sinc\left(\frac{\delta \omega T}{2}\right) cos\left(\frac {\delta \omega T}{2} + \delta\varphi\right) + n_{Ie}</math> | ||
| + | |||
| + | <math>I_{l} = A_{IQ} \rho\left(\delta \tau + \frac{\Delta \tau}{2}\right) sinc\left(\frac{\delta \omega T}{2}\right) cos\left(\frac {\delta \omega T}{2} + \delta\varphi\right) + n_{Il}</math> | ||
| + | |||
| + | Задача формирования шумов квадратурных сумм - абсолютно аналогична и независима, т.к. шумы между I и Q компонентами не коррелируют. | ||
== Многомерная нормальная СВ или вектор случайных величин? == | == Многомерная нормальная СВ или вектор случайных величин? == | ||
Версия 15:06, 21 августа 2013
При моделировании следящих систем НАП, а так же сигналов многоантенных НАП, возникает задача создания нормальных случайных величин с заданным коэффициентом корреляции.
Рассмотрим решение данной задачи на примере модели шумов статистического эквивалента корреляционных сумм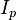 
, 
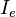и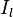 
.
Статистический эквивалент коррелятора
Статистический эквивалент коррелятора синфазных корреляционных сумм можно описать рядом выражений:
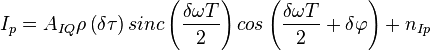
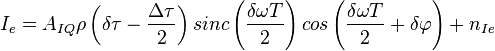
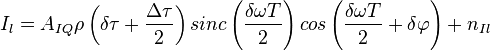
Задача формирования шумов квадратурных сумм - абсолютно аналогична и независима, т.к. шумы между I и Q компонентами не коррелируют.
Многомерная нормальная СВ или вектор случайных величин?
При синтезе радиотехнических систем часто используются модели, оперирующие с многомерными нормальными случайными величинами. Определение из Википедии:
Случайный векторимеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:
- Произвольная линейная комбинация компонентов вектора
имеет нормальное распределение или является константой.
- Существует вектор независимых стандартных нормальных случайных величин
, вещественный вектор
и матрица
размерности
, такие что:
.
- Существует вектор
и неотрицательно определённая симметричная матрица
размерности
, такие что характеристическая функция вектора
имеет вид:
.
Из первого условия следует, что каждая из компонент нормальной векторной СВ имеет нормальное распределение (для компоненты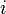 
это вытекает при 
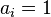и остальных коэффициентах комбинации, равных 0). Отсюда часто возникает иллюзия, что нормальность распределений компонент влечет нормальность совместного распределения. Этот тезис не выполняется, на контрпример можно взглянуть тут.
