Задание 2 к практическим занятиям (ММ РУиС) — различия между версиями

Версия 13:18, 17 марта 2014

Занятие 2

Тема занятия: Доплеровский сдвиг навигационного сигнала. Описание сигналов антенной решетки.

Цели занятия:

• развить навыки моделирования: использование векторов, цикл по времени, обработка результатов моделирование, построение графиков и гистограмм.

Задача 2.1 Расчет доплеровского сдвига навигационного сигнала

Постановка задачи:

Автомобильный навигатор является классическим радиоприемным устройством класса аппаратура потребителей спутниковых радионавигационных систем. В процессе своей работы он принимает сигналы от навигационных спутников, оценивает их параметры, выделяет навигационное сообщение, заложенное в сигналах, и, в итоге, решает навигационную задачу - определяет своё местоположение.

Так как навигационные спутники относительно планеты находятся в постоянном движении, да и из-за движения потребителя, возникает эффект Доплера - происходит смещение частоты принимаемого сигнала от номинала. Интересно, в каких пределах может находиться это смещение для неподвижного приемника? Какова гистограмма возможных значений?

Комментарии:

Связь доплеровского сдвига и скорости по линии визирования известна каждому радиотехнику:

.

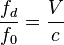Несущая частота 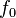радионавигационного сигнала известна, задается ИКД. Скорость света - фундаментальная константа. Остается определить скорость по линии визирования .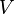

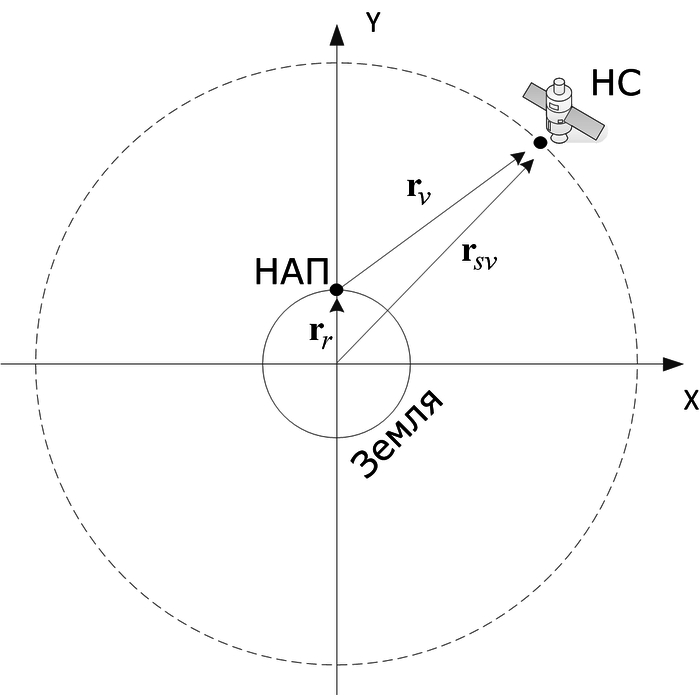
Потребитель по условию задачи неподвижен. Тогда скорость по линии визирования - проекция вектора скорости спутника на линию визирования. Итого, достаточно определить два вектора - орт от спутника к потребителю и вектор скорости спутника.

Для простоты ограничимся "плоской" задачей - когда потребитель попадает на подспутниковую траекторию, угловым вращением Земли так же пренебрежем. Иллюстрация - на рисунке:

Выберем СК XOY в которой потребитель расположен на оси OY, его радиус-вектор 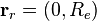, где 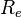- радиус Земли (учет высоты над уровнем моря для Москвы, 170-190 м, слабо повлияет на результат).

Если определим вектор спутника на любой момент витка, то задача будет почти решена, останется:

• выбрать те положения, для которых y-координата спутника больше y-координаты потребителя (условие видимости),
• по приращению координат определить вектор скорости спутника ,
• вычитанием найти вектор потребитель-спутник 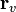задающий линию визирования,
• определить скорость сближения по линии визирования ,
• пересчитать скорость сближения в доплеровский сдвиг.

Определить же радиус-вектор спутника легко. Его длина известна, а скорость вращения - примерно оборот за 12 часов (у нас плоская задача, в которой мы пренебрегли различием ECEF и ECI).

Дальше - дело техники.

Шаги по усложнению модели, если результат неубедителен:

• учесть вращение Земли (наклонение орбит известно из ИКД),
• учесть случаи, когда потребитель не попадает под подспутниковую траекторию.