Дискриминатор частоты с временным сдвигом квадратурных компонент — различия между версиями

Версия 11:09, 30 октября 2015

Содержание

1 Особенности работы
2 Дискриминационная характеристика
3 Флуктуационная характеристика
4 Листинг модели
5 Ссылки

Дискриминатор частоты с временным сдвигом квадратурных компонент известен в англоязычной литературе как cross-product дискриминатор^[1].

Дискриминатор использует отсчеты коррелятора с текущего и предыдущего такта работы:

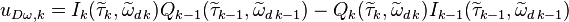$u_{D \omega, k} = I_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k})Q_{k-1}(\widetilde{\tau}_{k-1},\widetilde{\omega}_{d\,k-1}) - Q_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k})I_{k-1}(\widetilde{\tau}_{k-1},\widetilde{\omega}_{d\,k-1})$ ,

где

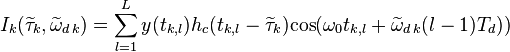$I_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)\mbox{cos}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))$ ,

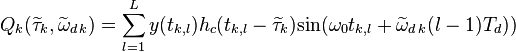$Q_k(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k)\mbox{sin}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))$ ,

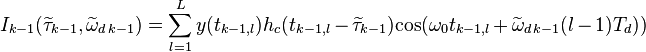$I_{k-1}(\widetilde{\tau}_{k-1},\widetilde{\omega}_{d\,{k-1}}) = \sum_{l=1}^{L}y(t_{k-1,l})h_{c}(t_{k-1,l}-\widetilde{\tau}_{k-1})\mbox{cos}(\omega_0t_{k-1,l}+\widetilde{\omega}_{d\,k-1}(l-1)T_d))$ ,

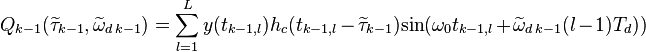$Q_{k-1}(\widetilde{\tau}_{k-1},\widetilde{\omega}_{d\,k-1}) = \sum_{l=1}^{L}y(t_{k-1,l})h_{c}(t_{k-1,l}-\widetilde{\tau}_{k-1})\mbox{sin}(\omega_0t_{k-1,l}+\widetilde{\omega}_{d\,k-1}(l-1)T_d))$ .

Особенности работы

Варианты работы дискриминатора

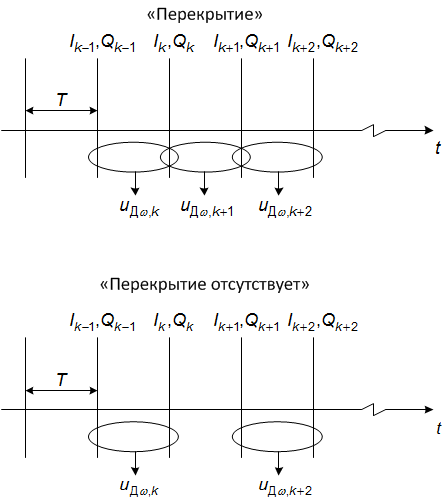
Возможны различные реализация дискриминатора. На рисунке представлено два варианта, условно названных "Перекрытие" и "Перекрытие отсутствует". Поясним рисунок.

Пусть в некоторый момент времени 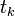$t_{k}$ доступны отсчеты с выхода коррелятора 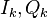$I_k, Q_k$ и отсчеты из предыдущей эпохи 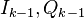$I_{k-1}, Q_{k-1}$ . На их основе можно сформировать отсчет дискриминатора 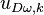$u_{D\omega,k}$ . Далее возможны варианты.

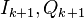В случае, если работа идет с "перекрытием", следующий отсчет дискриминатора $u_{D\omega,k+1}$ будет сформирован из новых отсчетов коррелятора $I_{k+1}, Q_{k+1}$ и уже использованных в предыдущем шаге 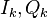$I_k, Q_k$ . Таким образом, каждое вычисление отсчета дискриминатора использует отсчеты коррелятора, уже использованные в расчете предыдущего значения дискриминатора. Поэтому шум выхода дискриминатора в данном случае оказывается коррелированным, а его СПМ отличается от СПМ белого шума.

Если дискриминатор работает без "перекрытия", для расчета соседних значений выхода дискриминатора каждый раз используются разные корреляционные суммы. В этом случае, шум дискриминатора будет некорреллированным с равномерной СПМ. Однако, темп работы такого дискриминатора ниже в 2 раза: ему нужно "дождаться" следующей пары отсчетов.

Для дискриминатора "с перекрытием" использование статистического эквивалента вида

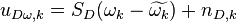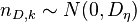
$u_{D\omega,k} = S_{D}(\omega_k - \widetilde{\omega_k}) + n_{D,k}$ , где $n_{D,k} \sim N(0, D_\eta)$

при моделировании следящих систем недопустимо, т.к. он не отражает корреляционных свойств. Следует воспользоваться статистическими эквивалентами коррелятора.

Дискриминационная характеристика

Сделано допущение, что $\varepsilon_{\omega,k-1} = \varepsilon_{\omega,k}$ .

$U(\varepsilon_\omega) = A_{IQ}^2\rho(\varepsilon_{\tau,k})\rho(\varepsilon_{\tau,k-1})\mbox{sinc}^2(\varepsilon_{\omega,k-1}T/2)\mbox{sin}(\varepsilon_{\omega,k-1}T),$

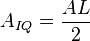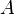где $A_{IQ} = \frac{AL}{2}$ , $A$ - амплитуда сигнала 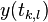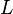$y(t_{k,l})$ , $L$ - количество отчетов, накапливаемых в корреляторе, $\varepsilon$ - разность истинного и опорного параметров.

Крутизна дискриминационной характеристики при нулевой расстройке по частоте: 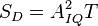$S_D = A_{IQ}^2T$ .

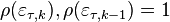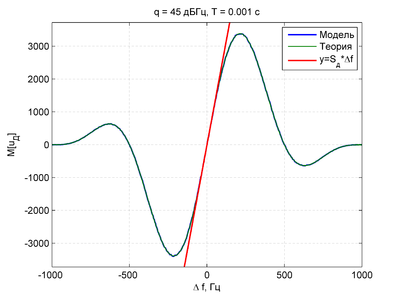
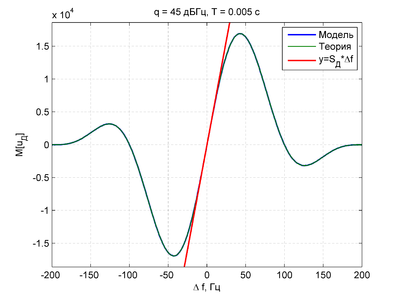
В модели задержка сигнала полагалась известной: $\rho(\varepsilon_{\tau,k}), \rho(\varepsilon_{\tau,k-1}) = 1$ .

Дискриминационная характеристика при различных временах накопления:

Дискриминационная характеристика при T=1 мс
Дискриминационная характеристика при T=5 мс

Флуктуационная характеристика

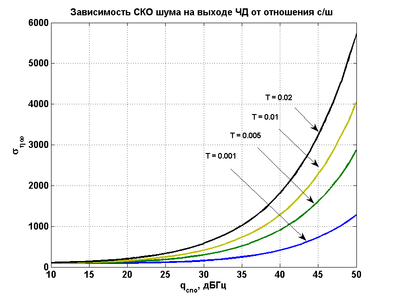
Получены зависимости СКО шума на выходе дискриминатора от 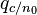$q_{c/n_0}$ для различных времен накопления. Теоретические кривые пунктирной линией.

Дисперсия шума эквивалентного наблюдения частоты, т.е. шума с выхода дискриминатора, пересчитанного к его входу при нулевой расстройке по частоте:

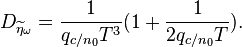
$D_{\widetilde{\eta}_\omega} = \frac{1}{q_{c/n_0}T^3}(1+\frac{1}{2q_{c/n_0}T}).$

Интересно сравнить дисперсию шумов по входу для разных дискриминаторов. На данный момент у нас есть:

Собственно дисперсия шума на входе рассматриваемого в этой статье дискриминатора. Обозначим ее как $D_1$ :

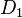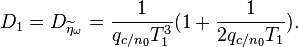
$D_1 = D_{\widetilde{\eta}_\omega} = \frac{1}{q_{c/n_0}T_1^3}(1+\frac{1}{2q_{c/n_0}T_1}).$

Дисперсия шума на входе оптимального при низком отношении сигнал/шум частотного дискриминатора (тот, который 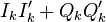$I_kI'_k+Q_kQ'_k$ ). Формула из диссера Корогодина И. В., или, например, из этой статьи. Обозначим ее как $D_2$ :

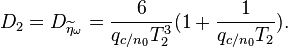
$D_2 = D_{\widetilde{\eta}_\omega} = \frac{6}{q_{c/n_0}T_2^3}(1+\frac{1}{q_{c/n_0}T_2}).$

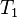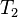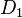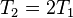Вообще говоря, время накопления в корреляторах может быть различно. Если принять равными времена $T_1$ и $T_2$ , получится что дискриминатору с временным сдвигом квадратур (c $D_1$ ) нужны будут квадратуры, накопленные на суммарном времени $2T_1$ и разбитые по времени пополам. Для корректности сравнения положим, что во втором дискриминаторе (у которого $D_2$ ) коррелятор копит на времени $T_2 = 2T_1$ . Разделим $D_2$ на $D_1$ . 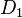После нехитрых вычислений окажется, что

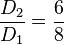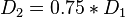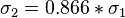$\frac{D_2}{D_1} = \frac{6}{8}$ , т. е. $D_2 = 0.75*D_1$ или для СКО: $\sigma_2 = 0.866*\sigma_1$ .

Таким образом, по дисперсии шумов наблюдается не очень то большая разница между сравниваемыми дискриминаторами. На рисунке ниже приведен график зависимости СКО эквивалентных шумов представленных ЧД от отношения сигнал/шум q_{c/n0}.

Ошибка создания миниатюры: convert: unable to open image `/app/images/0/07/20151029__.png': No such file or directory @ error/blob.c/OpenBlob/2641.
convert: no images defined `/tmp/transform_707878266798-1.png' @ error/convert.c/ConvertImageCommand/3044.

Листинг модели

Ниже представлен листинг модели, с которой сняты картинки.

Листинг модели

clear all
clc
close all

plotDX = 1; %считаем ДХ
plotFX = 0; %считаем дисперсию шумов

if plotDX
N = 3000;
stdn_IQ = 8;
Tc = 0.005;
qcno_dB = 45;
qcno = 10^(qcno_dB/10);

wdop_real = 2*pi*100;
wdop_oporn = [wdop_real-2*pi*(1/Tc):2*pi*(2/Tc)/500:wdop_real + 2*pi*(1/Tc)];

UdFLL = zeros(1, length(wdop_oporn));

A_IQ = stdn_IQ * sqrt(2 * qcno * Tc);
Sd = A_IQ^2*Tc;

for k = 1:N
for j = 1:length(wdop_oporn)
n_I_old = 1*stdn_IQ * randn(1,1);
n_I = 1*stdn_IQ * randn(1,1);
n_Q_old = 1*stdn_IQ * randn(1,1);
n_Q = 1*stdn_IQ * randn(1,1);

phi_real = [pi/3 pi/3 + Tc*wdop_real(1)];
phi_oporn =[pi/4 pi/4 + Tc*wdop_oporn(j)];

m_I_old = A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*cos(phi_real(1) - phi_oporn(1) + (wdop_real(1)-wdop_oporn(j))*Tc/2);

m_I = A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*cos(phi_real(2) - phi_oporn(2) + (wdop_real(1)-wdop_oporn(j))*Tc/2);

m_Q_old = - A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*sin(phi_real(1) - phi_oporn(1) + (wdop_real(1)-wdop_oporn(j))*Tc/2);

m_Q = - A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*sin(phi_real(2) - phi_oporn(2) + (wdop_real(1)-wdop_oporn(j))*Tc/2);

I_old = m_I_old + n_I_old;
I = m_I + n_I;
Q_old = m_Q_old + n_Q_old;
Q = m_Q + n_Q;

UdFLL(1, j) = UdFLL(1,j) + I*Q_old - Q*I_old;
end
if ~mod(k, N/10)
fprintf('Progress %d%%\n', k*100/N)
end
end

UdFLL_mean = A_IQ^2*(sinc((wdop_real(1)-wdop_oporn)*Tc/2 /pi)).^2.*sin((wdop_real(1)-wdop_oporn)*Tc);

UdFLL = UdFLL/N;

figure
plot((wdop_real-wdop_oporn)/2/pi,[UdFLL; UdFLL_mean; Sd*(wdop_real-wdop_oporn)]);
ylim([1.1*min(UdFLL_mean) 1.1*max(UdFLL_mean)])
grid on;
xlabel('\Delta f, Гц')
ylabel('M[u_{Д}]')
title(['q = ' num2str(qcno_dB) ' дБГц, T = ' num2str(Tc) ' c'])
end

if plotFX
N = 5000;
stdn_IQ = 8;
Tc = 0.02;
qcno_dB = [10:1:50];
wdop_real = [2*pi*100];
wdop_oporn = [2*pi*100];

D_etta_FLL = zeros(1,length(qcno_dB));
CKO_etta_FLL_teor = nan(1,length(qcno_dB));

for i = 1:length(qcno_dB)
fprintf('qcno_dB = %.0f\n', qcno_dB(i));
qcno = 10^(qcno_dB(i)/10);
A_IQ = stdn_IQ * sqrt(2 * qcno * Tc);

UdFLL = nan(1, N);

for k = 1:N

for j = 1:length(wdop_oporn)
n_I_old = 1*stdn_IQ * randn(1,1);
n_I = 1*stdn_IQ * randn(1,1);
n_Q_old = 1*stdn_IQ * randn(1,1);
n_Q = 1*stdn_IQ * randn(1,1);

phi_real = [pi/3 pi/3 + Tc*wdop_real(1)];
phi_oporn =[pi/4 pi/4 + Tc*wdop_oporn(j)];
m_I_old = A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*cos(phi_real(1) - phi_oporn(1) + (wdop_real(1)-wdop_oporn(j))*Tc/2);

m_I = A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*cos(phi_real(2) - phi_oporn(2) + (wdop_real(1)-wdop_oporn(j))*Tc/2);

m_Q_old = - A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*sin(phi_real(1) - phi_oporn(1) + (wdop_real(1)-wdop_oporn(j))*Tc/2);

m_Q = - A_IQ * sinc((wdop_real(1)-wdop_oporn(j))*Tc/2 /pi)*sin(phi_real(2) - phi_oporn(2) + (wdop_real(1)-wdop_oporn(j))*Tc/2);

I_old = m_I_old + n_I_old;
I = m_I + n_I;
Q_old = m_Q_old + n_Q_old;
Q = m_Q + n_Q;

UdFLL(1, k) = I*Q_old - Q*I_old;
end
end
D_etta_FLL(1,i) = mean((UdFLL - mean(UdFLL)).^2);

CKO_etta_FLL(1,i) = sqrt(D_etta_FLL(1,i));
CKO_etta_FLL_teor(1,i) = sqrt((A_IQ^2*Tc)^2*(1/(qcno*Tc^3))*(1 + 1/(2*qcno*Tc)));
end
figure
plot(qcno_dB, CKO_etta_FLL, 'r*', qcno_dB, CKO_etta_FLL_teor, 'g')
xlabel('q_c/n0, дБГц')
ylabel('\sigma_{вых} ЧД')
grid on
end

Ссылки

↑ http://www.navipedia.net/index.php/Frequency_Lock_Loop_(FLL)

[NavipediaFLL-0] ttp://www.navipedia.net/index.php/Frequency_Lock_Loop_(FLL)

[1]

@@ Строка 16: / Строка 16: @@
 == Особенности работы ==
 [[Файл:20151028_Про перекрытие.png|мини|справа|600пкс|Варианты работы дискриминатора]]
-Отметим, что возможна различная интерпретация работы дискриминатора. На рисунке представлено два возможных варианта, условно названных "Перекрытие" и "Перекрытие отсутствует". Поясним рисунок. Пусть в некоторый момент времени <math>t_{k}</math> доступны отсчеты с выхода коррелятора <math>I_k, Q_k</math> и отсчеты из предыдущей эпохи <math>I_{k-1}, Q_{k-1}</math>. На их основе можно сформировать отсчет дискриминатора <math>u_{D\omega,k}</math>. Далее возможны варианты. В случае, если работа идет с "перекрытием", следующий отсчет дискриминатора <math>u_{D\omega,k+1}</math> будет сформирован из новых отсчетов коррелятора <math>I_{k+1}, Q_{k+1}</math> и уже использованных в предыдущем шаге <math>I_k, Q_k</math>. Таким образом, каждое вычисление отсчета дискриминатора использует отсчеты коррелятора, уже использованные в расчете предыдущего значения дискриминатора. Поэтому шум выхода дискриминатора в данном случае оказывается коррелированным, а его СПМ отличается от СПМ белого шума.  В случае работы без "перекрытия" для расчета соседних значений выхода дискриминатора каждый раз используются разные корреляционные суммы. В этом случае, шум дискриминатора будет некорреллированным с равномерной СПМ. Однако, темп работы такого дискриминатора ниже в 2 раза: ему нужно "дождаться" следующей пары отсчетов.
-Формулы для крутизны и дисперсии шумов на выходе/входе ЧД (приведены далее) позволяют моделировать его в виде стат. эквивалента
+Возможны различные реализация дискриминатора. На рисунке представлено два варианта, условно названных "Перекрытие" и "Перекрытие отсутствует". Поясним рисунок.
-<math>u_{D\omega,k} = S_{D}(\omega_k - \widetilde{\omega_k}) + n_{D,k}</math>, где <math>n_{D,k} \sim N(0, D_\eta)</math>
+Пусть в некоторый момент времени <math>t_{k}</math> доступны отсчеты с выхода коррелятора <math>I_k, Q_k</math> и отсчеты из предыдущей эпохи <math>I_{k-1}, Q_{k-1}</math>. На их основе можно сформировать отсчет дискриминатора <math>u_{D\omega,k}</math>. Далее возможны варианты.
+В случае, если работа идет с "перекрытием", следующий отсчет дискриминатора <math>u_{D\omega,k+1}</math> будет сформирован из новых отсчетов коррелятора <math>I_{k+1}, Q_{k+1}</math> и уже использованных в предыдущем шаге <math>I_k, Q_k</math>. Таким образом, каждое вычисление отсчета дискриминатора использует отсчеты коррелятора, уже использованные в расчете предыдущего значения дискриминатора. Поэтому шум выхода дискриминатора в данном случае оказывается коррелированным, а его СПМ отличается от СПМ белого шума.
+Если дискриминатор работает без "перекрытия", для расчета соседних значений выхода дискриминатора каждый раз используются разные корреляционные суммы. В этом случае, шум дискриминатора будет некорреллированным с равномерной СПМ. Однако, темп работы такого дискриминатора ниже в 2 раза: ему нужно "дождаться" следующей пары отсчетов.
+Для дискриминатора "с перекрытием" использование статистического эквивалента вида
+:<math>u_{D\omega,k} = S_{D}(\omega_k - \widetilde{\omega_k}) + n_{D,k}</math>, где <math>n_{D,k} \sim N(0, D_\eta)</math>
+при моделировании следящих систем недопустимо, т.к. он не отражает корреляционных свойств. Следует воспользоваться статистическими эквивалентами коррелятора.
-Стоит отметить, что моделирование по этим формулам нужно проводить для случая "перекрытие отсутствует", т. к. в случае с "перекрытием" необходимо будет моделировать корреллированность шумов во временных отсчетах дискриминатора.
 <br clear="all" />

Дискриминатор частоты с временным сдвигом квадратурных компонент — различия между версиями

Версия 11:09, 30 октября 2015

Содержание

Особенности работы

Дискриминационная характеристика

Флуктуационная характеристика

Листинг модели

Ссылки

Персональные инструменты

Пространства имён

Варианты

Просмотры

Действия

Поиск

SRNS Wiki

Рабочие журналы

Приватный файлсервер

QNAP Сервер

Инструменты