Поиск навигационного сигнала (лабораторная работа) — различия между версиями
Korogodin (обсуждение | вклад) (Новая страница: «== Цели работы == * Составить представление о подходах моделирования работы алгоритмов обр...») |
Korogodin (обсуждение | вклад) (→Описание) |
||
| Строка 17: | Строка 17: | ||
Для осуществления процедуры поиска используются корреляционные свойства сигнала. | Для осуществления процедуры поиска используются корреляционные свойства сигнала. | ||
| + | |||
| + | == Модель блока поиска и входных сигналов == | ||
| + | |||
| + | Для проведения имитационного моделирования необходимо: | ||
| + | * Составить модель исследуемого алгоритма поиска | ||
| + | * Составить модель сигналов, с помощью которых будет проводиться тестирование работы алгоритма поиска (т.н. testbench) | ||
| + | |||
| + | Для реализации поставленной задачи воспользуемся средой Matlab. Код модели разместим в двух файлах: | ||
| + | * <code>main.m</code> - главный скрипт модели, с которого начинается исполнение | ||
| + | * <code>resize_arr.m</code> - файл, содержащий код ''функции'' передискретизации вектора | ||
| + | |||
| + | Средствами Matlab легко сохранять полученные данные. В прошлой лабораторной работе была рассчитана M-последовательность, используемая в качестве дальномерного кода гражданских сигналов системы ГЛОНАСС. Вектор её 511 символов сохранен в файл <code>MCode.mat</code>. Символы принимают значения <math>\pm 1</math>. Воспользуемся этим файлом в ходе работы. | ||
| + | |||
| + | 1. Создайте файл main.m. Внесите первые строчки кода: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | clc % Очистить Command Window | ||
| + | clear % Очистить список переменных и вернуть системе память, выделенную для них | ||
| + | close all % Закрыть все объекты типа figure | ||
| + | </source> | ||
| + | |||
| + | Запуск скрипта сохранит изменения в файле, после чего произведет соответствующие коду действия. | ||
| + | |||
| + | 2. Зададим ось времени | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | Tc = 0.001; % Период ПСП = период когерентного субнакопления | ||
| + | Fd = 10*5.11e6; % Частота дискретизации на выходе АЦП | ||
| + | Td = 1/Fd; % Период дискретизации на выходе АЦП | ||
| + | |||
| + | t = Td:Td:Tc; % Моменты взятия отсчетов АЦП. Команда Td:Td:Tc возвращает вектор-строку от Td с шагом Td до Tc. | ||
| + | C = length(t); % Число элементов в векторе-строке t | ||
| + | </source> | ||
| + | |||
| + | Запустите скрипт. | ||
| + | |||
| + | N_fft = 1022; % Размерность БПФ | ||
| + | |||
| + | |||
| + | load MCode.mat | ||
| + | L_psp = length(MCode); % Длина ПСП | ||
| + | |||
| + | |||
| + | % Модель сигнала АЦП | ||
| + | f_if = 10.8e6; % Промежуточная частота для сигнала ГЛОНАСС с литерой 0. | ||
| + | w_if = 2*pi*f_if; | ||
| + | max_f_dop = 10e3; | ||
| + | f_dop = max_f_dop * 2*(rand(1,1) - 0.5); % Доплер - СВ +/- 10кГц | ||
| + | w_dop = 2*pi*f_dop; | ||
| + | |||
| + | |||
| + | MCode_C = resize_array(MCode, C); % ПСП с частотой дискретизации АЦП и нулевой задержкой | ||
| + | tau_C = round(C*rand(1,1)); % Задержка в тактах АЦП - СВ с равномерным распределением | ||
| + | MCode_C_shifted = circshift(MCode_C, [0 tau_C]); % Задержанное ПСП | ||
| + | tau_chip = tau_C / C * L_psp; % Задержка, измеренная в чипах ПСП; | ||
| + | |||
| + | |||
| + | phase0 = rand(1,1)*2*pi; % Начальная фаза | ||
| + | Phase = w_if*t + w_dop*t + phase0; % Полная фаза на выходе АЦП | ||
| + | |||
| + | |||
| + | stdn = 22; % СКО шума на выходе АЦП | ||
| + | qcno_dBHz = 55; % Отношение сигнал/шум в дБГц | ||
| + | qcno = 10^(qcno_dBHz/10); | ||
| + | A = 2*stdn*sqrt(qcno*Td); % Амплитуда сигнала на выходе АЦП для данных параметров | ||
| + | |||
| + | |||
| + | y_adc = A*cos(Phase + MCode_C_shifted*pi) + stdn*randn(1,C); % Сигнал на выходе АЦП без учета ЦИ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | hF = 0; | ||
| + | hF = figure(hF + 1); | ||
| + | plot(t, y_adc); | ||
| + | xlabel('t, s'); | ||
| + | ylabel('y_{ADC}'); | ||
| + | |||
| + | |||
| + | % Модель преднакопления | ||
| + | Npr = 50; % Число точек преднакопления | ||
| + | Ipr = zeros(1, N_fft); Qpr = zeros(1, N_fft); % Инициализация нулями | ||
| + | n = 1:N_fft; | ||
| + | |||
| + | |||
| + | cos_op_pr = cos(w_if*t); | ||
| + | sin_op_pr = sin(w_if*t); | ||
| + | for j = 1:N_fft | ||
| + | for npr = 1:Npr | ||
| + | index_pr = Npr*(j-1) + npr; | ||
| + | Ipr(j) = Ipr(j) + y_adc(index_pr).*cos_op_pr(index_pr); | ||
| + | Qpr(j) = Qpr(j) + y_adc(index_pr).*sin_op_pr(index_pr); | ||
| + | end | ||
| + | end | ||
| + | |||
| + | |||
| + | hF = figure(hF+1); | ||
| + | plot(n, Ipr, n, Qpr); | ||
| + | xlabel('n') | ||
| + | ylabel('I_{pr}, Q_{pr}') | ||
| + | xlim([1 N_fft]) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | % Ячейки по частоте и задержке | ||
| + | dFdop_s = 1/5 * 2/3 * 1/Tc; % Шаг по частоте | ||
| + | Fdop_s = -max_f_dop:dFdop_s:max_f_dop; | ||
| + | s_Fdop_s = length(Fdop_s); | ||
| + | |||
| + | |||
| + | IQ_pole = nan(s_Fdop_s, N_fft); % Инициализациия поверхности поля поиска | ||
| + | |||
| + | |||
| + | MCode_N_fft = resize_array(MCode, N_fft); % ПСП ДК с для свертки | ||
| + | fft_MCode = conj(fft(MCode_N_fft)); | ||
| + | |||
| + | |||
| + | i = sqrt(-1); | ||
| + | for j = 1:s_Fdop_s | ||
| + | t_j = (Npr*Td)*n; | ||
| + | cos_op = cos(2*pi*Fdop_s(j)*t_j); | ||
| + | sin_op = sin(2*pi*Fdop_s(j)*t_j); | ||
| + | Sig = (Ipr - 1i*Qpr) .* (cos_op + 1i*sin_op);%Ipr.*cos_op - i*Qpr.*sin_op; | ||
| + | pole_row = ifft( fft(Sig) .* fft_MCode ); | ||
| + | IQ_pole(j, :) = pole_row; | ||
| + | end | ||
| + | |||
| + | |||
| + | hF = figure(hF + 1); | ||
| + | if s_Fdop_s > 1 | ||
| + | mesh((n-1)/(N_fft-1)*L_psp, Fdop_s, abs(IQ_pole)/max(max(abs(IQ_pole)))); | ||
| + | xlabel('\tau, chips') | ||
| + | ylabel('Fdop, Hz') | ||
| + | else | ||
| + | plot((n-1)/(N_fft-1)*L_psp, abs(IQ_pole) / max(abs(IQ_pole))); | ||
| + | xlabel('\tau, chips') | ||
| + | ylabel('abs(IQ)') | ||
| + | end | ||
| + | |||
| + | |||
| + | fprintf('Real delay = %.3f, chips\n', tau_chip); | ||
| + | fprintf('Real dopler = %.3f, Hz\n', f_dop); | ||
Текущая версия на 18:04, 10 апреля 2012
Содержание |
[править] Цели работы
- Составить представление о подходах моделирования работы алгоритмов обработки сигналов в НАП
- Проверить работоспособность алгоритма поиска сигналов, изложенного на лекционных занятиях
[править] Состав стенда
Для выполнения лабораторной работы необходим персональный компьютер с ОС семейства Linux или Windows с установленным пакетом ПО Matlab.
[править] Описание
Как известно из курса радиоавтоматики, системы слежения обладают конечной полосой захвата. Поэтому после включения приемника, либо появления нового спутника в области радиовидимости, необходимо произвести передачу целеуказания системам слежения - сообщить примерные параметры частоты и задержки сигнала.
Поиск - это этап обработки навигационного радиосигнала, целью которого является грубое определение параметров с точностью, достаточной для осуществления захвата системами слежения. Конкретная величина допустимой погрешности определяется применяемыми алгоритмами, но характерный порядок - десятые доли символа дальномерного кода для оценки задержки и сотни герц для системы слежения за частотой.
Для осуществления процедуры поиска используются корреляционные свойства сигнала.
[править] Модель блока поиска и входных сигналов
Для проведения имитационного моделирования необходимо:
- Составить модель исследуемого алгоритма поиска
- Составить модель сигналов, с помощью которых будет проводиться тестирование работы алгоритма поиска (т.н. testbench)
Для реализации поставленной задачи воспользуемся средой Matlab. Код модели разместим в двух файлах:
-
main.m- главный скрипт модели, с которого начинается исполнение -
resize_arr.m- файл, содержащий код функции передискретизации вектора
Средствами Matlab легко сохранять полученные данные. В прошлой лабораторной работе была рассчитана M-последовательность, используемая в качестве дальномерного кода гражданских сигналов системы ГЛОНАСС. Вектор её 511 символов сохранен в файл MCode.mat. Символы принимают значения 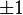 . Воспользуемся этим файлом в ходе работы.
. Воспользуемся этим файлом в ходе работы.
1. Создайте файл main.m. Внесите первые строчки кода:
clear % Очистить список переменных и вернуть системе память, выделенную для них
close all % Закрыть все объекты типа figure
Запуск скрипта сохранит изменения в файле, после чего произведет соответствующие коду действия.
2. Зададим ось времени
Fd = 10*5.11e6; % Частота дискретизации на выходе АЦП
Td = 1/Fd; % Период дискретизации на выходе АЦП
t = Td:Td:Tc; % Моменты взятия отсчетов АЦП. Команда Td:Td:Tc возвращает вектор-строку от Td с шагом Td до Tc.
C = length(t); % Число элементов в векторе-строке t
Запустите скрипт.
N_fft = 1022; % Размерность БПФ
load MCode.mat
L_psp = length(MCode); % Длина ПСП
% Модель сигнала АЦП
f_if = 10.8e6; % Промежуточная частота для сигнала ГЛОНАСС с литерой 0.
w_if = 2*pi*f_if;
max_f_dop = 10e3;
f_dop = max_f_dop * 2*(rand(1,1) - 0.5); % Доплер - СВ +/- 10кГц
w_dop = 2*pi*f_dop;
MCode_C = resize_array(MCode, C); % ПСП с частотой дискретизации АЦП и нулевой задержкой
tau_C = round(C*rand(1,1)); % Задержка в тактах АЦП - СВ с равномерным распределением
MCode_C_shifted = circshift(MCode_C, [0 tau_C]); % Задержанное ПСП
tau_chip = tau_C / C * L_psp; % Задержка, измеренная в чипах ПСП;
phase0 = rand(1,1)*2*pi; % Начальная фаза
Phase = w_if*t + w_dop*t + phase0; % Полная фаза на выходе АЦП
stdn = 22; % СКО шума на выходе АЦП
qcno_dBHz = 55; % Отношение сигнал/шум в дБГц
qcno = 10^(qcno_dBHz/10);
A = 2*stdn*sqrt(qcno*Td); % Амплитуда сигнала на выходе АЦП для данных параметров
y_adc = A*cos(Phase + MCode_C_shifted*pi) + stdn*randn(1,C); % Сигнал на выходе АЦП без учета ЦИ
hF = 0;
hF = figure(hF + 1);
plot(t, y_adc);
xlabel('t, s');
ylabel('y_{ADC}');
% Модель преднакопления
Npr = 50; % Число точек преднакопления
Ipr = zeros(1, N_fft); Qpr = zeros(1, N_fft); % Инициализация нулями
n = 1:N_fft;
cos_op_pr = cos(w_if*t);
sin_op_pr = sin(w_if*t);
for j = 1:N_fft
for npr = 1:Npr
index_pr = Npr*(j-1) + npr;
Ipr(j) = Ipr(j) + y_adc(index_pr).*cos_op_pr(index_pr);
Qpr(j) = Qpr(j) + y_adc(index_pr).*sin_op_pr(index_pr);
end
end
hF = figure(hF+1);
plot(n, Ipr, n, Qpr);
xlabel('n')
ylabel('I_{pr}, Q_{pr}')
xlim([1 N_fft])
% Ячейки по частоте и задержке
dFdop_s = 1/5 * 2/3 * 1/Tc; % Шаг по частоте
Fdop_s = -max_f_dop:dFdop_s:max_f_dop;
s_Fdop_s = length(Fdop_s);
IQ_pole = nan(s_Fdop_s, N_fft); % Инициализациия поверхности поля поиска
MCode_N_fft = resize_array(MCode, N_fft); % ПСП ДК с для свертки
fft_MCode = conj(fft(MCode_N_fft));
i = sqrt(-1);
for j = 1:s_Fdop_s
t_j = (Npr*Td)*n; cos_op = cos(2*pi*Fdop_s(j)*t_j); sin_op = sin(2*pi*Fdop_s(j)*t_j); Sig = (Ipr - 1i*Qpr) .* (cos_op + 1i*sin_op);%Ipr.*cos_op - i*Qpr.*sin_op; pole_row = ifft( fft(Sig) .* fft_MCode ); IQ_pole(j, :) = pole_row;
end
hF = figure(hF + 1);
if s_Fdop_s > 1
mesh((n-1)/(N_fft-1)*L_psp, Fdop_s, abs(IQ_pole)/max(max(abs(IQ_pole))));
xlabel('\tau, chips')
ylabel('Fdop, Hz')
else
plot((n-1)/(N_fft-1)*L_psp, abs(IQ_pole) / max(abs(IQ_pole)));
xlabel('\tau, chips')
ylabel('abs(IQ)')
end
fprintf('Real delay = %.3f, chips\n', tau_chip);
fprintf('Real dopler = %.3f, Hz\n', f_dop);