Дискриминатор задержки NELP — различия между версиями
Dneprov (обсуждение | вклад) (Новая страница: «=Описание дискриминатора= Non-coherent Early minus Late Power (NELP) - некогерентный дискриминатор задержк…») |
|||
| (не показаны 15 промежуточных версий 3 участников) | |||
| Строка 5: | Строка 5: | ||
где <br /> | где <br /> | ||
| − | <math> | + | <math>I_{E,k}(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k+\frac{\Delta\tau}{2})\mbox{cos}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))</math>,<br /> |
| − | <math> | + | <math>I_{L,k}(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k-\frac{\Delta\tau}{2})\mbox{cos}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))</math>,<br /> |
| − | <math> | + | <math>Q_{E,k}(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k+\frac{\Delta\tau}{2})\mbox{sin}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))</math>,<br /> |
| − | <math>Q_{k | + | <math>Q_{L,k}(\widetilde{\tau}_k,\widetilde{\omega}_{d\,k}) = \sum_{l=1}^{L}y(t_{k,l})h_{c}(t_{k,l}-\widetilde{\tau}_k-\frac{\Delta\tau}{2})\mbox{sin}(\omega_0t_{k,l}+\widetilde{\omega}_{d\,k}(l-1)T_d))</math>. <br /> |
| + | |||
| + | <math>\Delta\tau</math> - сдвиг дальномерного кода между запаздывающей и опережающей компонентами. | ||
| + | |||
| + | == Дискриминационная характеристика == | ||
| + | Дискриминационная характеристика описывается выражением (для квадратур с единичной дисперсией) <br /> | ||
| + | <math>U(\varepsilon_\tau) = 2q_{c/n0}T\mbox{sinc}^2(\varepsilon_{\omega,k}T/2)\left ( \rho\left (\varepsilon_\tau - \frac{\Delta\tau}{2} \right )^2 - \rho\left (\varepsilon_\tau + \frac{\Delta\tau}{2} \right )^2 \right )</math>. | ||
| + | |||
| + | Ее крутизна <math>S_d = 2q_{c/n0}T\mbox{sinc}^2(\varepsilon_{\omega,k}T/2)\left ( \frac{4}{\tau_{chip}} - \frac{2\Delta\tau}{\tau_{chip}^2} \right ) </math>. | ||
| + | |||
| + | |||
| + | Для проверки формул составлена модель в Matlab. | ||
| + | В модели принято: <br /> | ||
| + | * длительность символа дальномерного кода <math>{{\tau }_{chip}} = 2</math> мкс, <br /> | ||
| + | * расстройка по частоте <math>{{\varepsilon }_{\omega }}=10</math> Гц, | ||
| + | * каждая точка моделируемой дискриминационной характеристики усреднялась 1000 раз, | ||
| + | * корреляционная функция дальномерного кода соответствует сигналу с BPSK : <math>\rho \left( {{\varepsilon }_{\tau }} \right)=1-\frac{\left| {{\varepsilon }_{\tau }} \right|}{{{\tau }_{chip}}}</math>; | ||
| + | * коррелированность шумов квадратур E, P, L моделируется с помощью [[Моделирование коррелированных гауссовых СВ|разложения Холецкого.]] | ||
| + | |||
| + | |||
| + | Результат моделирования для <math>{q}_{c/n0}=45</math> дБГц, <math>T=1</math> мс, <math>\Delta \tau ={{\tau }_{chip}}</math>: | ||
| + | |||
| + | [[File:20140327 DZO q45,T=1ms,delta=chip.png|center|600px]] | ||
| + | |||
| + | |||
| + | Результаты моделирования для <math>{q}_{c/n0}=45</math> дБГц, <math>T=1</math> мс, <math>\Delta \tau =\frac{\tau_{chip}}{10}</math>: | ||
| + | |||
| + | [[File:20140327 DZO q45,T=1ms,delta=0.1chip.png|center|600px]] | ||
| + | |||
| + | |||
| + | Результаты моделирования для <math>{q}_{c/n0}=35</math> дБГц, <math>T=20</math> мс, <math>\Delta \tau =\frac{\tau_{chip}}{5}</math>: | ||
| + | |||
| + | [[File:20140327 DZO q35,T=20ms,delta=chip5.png|center|600px]] | ||
| + | |||
| + | == Флуктуационная характеристика == | ||
| + | |||
| + | Флуктуационная характеристика описывается выражением<br /> | ||
| + | |||
| + | <math>D_{u\tau }^{{}}=\left( 1-\rho ^{{}}\left( \Delta \tau \right) \right)16q_{c/n0}^{{}}T\sigma _{IQ}^{4}\left( \rho ^{2}\left( \frac{\Delta \tau }{2} \right)+\frac{1+\rho \left( \Delta \tau \right)}{2q_{c/n0}^{{}}T} \right)</math>. | ||
| + | |||
| + | Дисперсия шума эквивалентного наблюдения, т.е. шума с выхода дискриминатора, пересчитанного к его входу при нулевой расстройке <br /> | ||
| + | |||
| + | <math>D_{\tilde{u}\tau }^{{}}=\frac{D_{u\tau }^{{}}}{S{{_{d}^{{}}}^{2}}}=\frac{4\left( 1-\rho \left( \Delta \tau \right) \right)\left( \rho ^{2}\left( \frac{\Delta \tau }{2} \right)+\frac{1+\rho \left( \Delta \tau \right)}{2q_{c/n0}^{{}}T} \right)}{2q_{c/n0}^{{}}{{T}^{{}}}{{\left( \frac{2}{\tau _{chip}^{{}}}-\frac{{}^{\Delta \tau }/{}_{2}}{\tau _{chip}^{2}} \right)}^{2}}}</math> | ||
| + | |||
| + | |||
| + | Аналитические выражения проверены на модели. <br /> | ||
| + | В модели принято: <br /> | ||
| + | |||
| + | * длительность символа дальномерного кода <math>{{\tau }_{chip}}=\frac{1}{511}</math> мс, <br /> | ||
| + | * время накопления коррелятора <math>{{T }_{c }}=3</math> мс, | ||
| + | * усреднение проводилось по 5000 реализациям, | ||
| + | * расстройка по частоте <math>{{\varepsilon }_{\omega }}=10</math> Гц, | ||
| + | * корреляционная функция дальномерного кода соответствует сигналу с BPSK : <math>\rho \left( {{\varepsilon }_{\tau }} \right)=1-\frac{\left| {{\varepsilon }_{\tau }} \right|}{{{\tau }_{chip}}}</math>; | ||
| + | * коррелированность шумов квадратур E, P, L моделируется с помощью [[Моделирование коррелированных гауссовых СВ|разложения Холецкого.]]<br /> | ||
| + | |||
| + | |||
| + | Результаты моделирования:<br /> | ||
| + | |||
| + | Зависимость СКО шума на выходе дискриминатора от отношения сигнал/шум при <math>\Delta \tau =\frac{\tau_{chip}}{10}</math>:<br /> | ||
| + | |||
| + | [[File:20200511_dep_Du_qcn0_NELP.png|center|600px]] | ||
| + | |||
| + | Зависимость СКО эквивалентных шумов от отношения сигнал/шум при <math>\Delta \tau =\frac{\tau_{chip}}{10}</math>:<br /> | ||
| + | |||
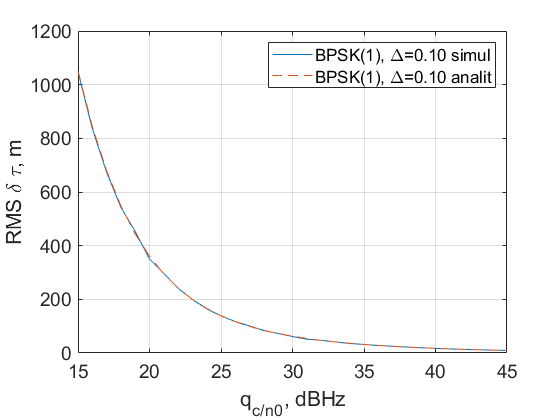
| + | [[File:20200511_dep_Du_Sd2_qcn0_NELP.png|center|600px]] | ||
| + | |||
| + | |||
| + | {{Hider | ||
| + | |title = Листинг модели | ||
| + | |content = <source lang = matlab> | ||
| + | Файл ro.m | ||
| + | |||
| + | function r = ro( x ) | ||
| + | |||
| + | global tauChip; | ||
| + | r = (abs(x) < tauChip).*(1 - abs(x)./tauChip); | ||
| + | |||
| + | |||
| + | end | ||
| + | |||
| + | |||
| + | Файл main.m | ||
| + | |||
| + | close all; | ||
| + | clear | ||
| + | clc | ||
| + | |||
| + | global tauChip | ||
| + | tauChip = 1e-3/511; % Длительность чипа | ||
| + | |||
| + | NoiseEnable = 1; | ||
| + | |||
| + | Np = 1000; | ||
| + | |||
| + | Tc = 0.001; % Период интегрирования в корреляторе | ||
| + | |||
| + | qcno_dB = 45; | ||
| + | stdn_IQ = 1; % СКО шума квадратурных сумм | ||
| + | |||
| + | qcno = 10^(qcno_dB/10); | ||
| + | A_IQ = stdn_IQ * sqrt(2 * qcno * Tc); | ||
| + | |||
| + | tauIst = tauChip/5; | ||
| + | deltaTau = tauChip/10; | ||
| + | |||
| + | Dp=stdn_IQ^2; % Дисперсия promt компоненты | ||
| + | Dpe=ro(deltaTau/2)*stdn_IQ^2; % Взаимная дисперсия promt-early/late | ||
| + | Del=ro(deltaTau)*stdn_IQ^2; % Взаимная дисперсия early-late | ||
| + | |||
| + | L=chol([Dp Dpe Dpe; % Используем разложение Холецкого | ||
| + | Dpe Dp Del; | ||
| + | Dpe Del Dp])'; | ||
| + | |||
| + | |||
| + | tauExtr= [tauIst-2*tauChip:4*tauChip/1000:tauIst+2*tauChip]; | ||
| + | NtauExtr = length(tauExtr); | ||
| + | |||
| + | EpsPhi = 1*rand(1,1)*2*pi; | ||
| + | EpsW = 1*10*2*pi; | ||
| + | |||
| + | SdTeor = 2*qcno*Tc*sinc(EpsW*Tc/2 /pi)^2*(4/tauChip - 2*(deltaTau/tauChip^2)); % Теоретическая крутизна | ||
| + | |||
| + | Ud = zeros(1,NtauExtr); | ||
| + | Udteor = zeros(1,NtauExtr); | ||
| + | |||
| + | p = nan(1,NtauExtr); | ||
| + | p_early = nan(1,NtauExtr); | ||
| + | p_late = nan(1,NtauExtr); | ||
| + | EpsTau = nan(1,NtauExtr); | ||
| + | |||
| + | for k = 1:NtauExtr | ||
| + | |||
| + | EpsTau(k) = tauIst - tauExtr(k); | ||
| + | |||
| + | p(k) = ro(EpsTau(k)); | ||
| + | p_late(k) = ro(EpsTau(k)+deltaTau/2); | ||
| + | p_early(k) = ro(EpsTau(k)-deltaTau/2); | ||
| + | |||
| + | for n = 1:Np | ||
| + | |||
| + | nI = L * randn(3,1); % Применяем результат разложения Холецкого и получаем коррелированные шумы | ||
| + | nQ = L* randn(3,1); | ||
| + | |||
| + | mI = A_IQ * p(k) * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | mIe = A_IQ*p_early(k) * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | mIl = A_IQ*p_late(k) *sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | |||
| + | mQ = -A_IQ * p(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | mQe = -A_IQ*p_early(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | mQl = -A_IQ*p_late(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | |||
| + | I = mI + NoiseEnable*nI(1,1); | ||
| + | Ie = mIe + NoiseEnable*nI(2,1); | ||
| + | Il = mIl + NoiseEnable*nI(3,1); | ||
| + | Q = mQ + NoiseEnable*nQ(1,1); | ||
| + | Qe = mQe + NoiseEnable*nQ(2,1); | ||
| + | Ql = mQl + NoiseEnable*nQ(3,1); | ||
| + | |||
| + | Ud(k) = Ud(k) + (Ie^2-Il^2) + (Qe^2-Ql^2); | ||
| + | end | ||
| + | Udteor(k) = 2*qcno*Tc*(sinc(EpsW*Tc/2 /pi)^2)*(p_early(k)^2 - p_late(k)^2); | ||
| + | if ~mod(k,100) | ||
| + | fprintf('Progress: %.2f %%\n', k*100/NtauExtr) | ||
| + | end | ||
| + | end | ||
| + | |||
| + | plot(EpsTa[[:File:20200511_dep_Du_Sd2_qcn0_NELP.png]]u/tauChip, [Ud/Np; Udteor; SdTeor*EpsTau]) | ||
| + | xlabel('\epsilon_{tau}/\tau_{chip}') | ||
| + | ylim([min(Udteor)-10 max(Udteor)+10]) | ||
| + | grid on | ||
| + | |||
| + | |||
| + | Файл fluct.m | ||
| + | |||
| + | close all; clear; clc | ||
| + | |||
| + | global tauChip | ||
| + | tauChip = 1e-3/511; % Длительность чипа | ||
| + | |||
| + | LightC = 3e8; | ||
| + | NoiseEnable = 1; | ||
| + | |||
| + | Np = 5000; | ||
| + | Tc = 3e-3; % Период интегрирования в корреляторе | ||
| + | |||
| + | qcno_dB = 15:1:45; | ||
| + | qcno = 10.^(qcno_dB/10); | ||
| + | stdn_IQ = 13; % СКО шума квадратурных сумм | ||
| + | A_IQ = stdn_IQ * sqrt(2 * qcno * Tc); | ||
| + | |||
| + | tauIst =tauChip*rand(1,1); | ||
| + | deltaTau = tauChip/10; | ||
| + | |||
| + | Dp=stdn_IQ^2; % Дисперсия promt компоненты | ||
| + | Dpe=ro(deltaTau/2)*stdn_IQ^2; % Взаимная дисперсия promt-early/late | ||
| + | Del=ro(deltaTau)*stdn_IQ^2; % Взаимная дисперсия early-late | ||
| + | |||
| + | L=chol([Dp Dpe Dpe; % Используем разложение Холецкого | ||
| + | Dpe Dp Del; | ||
| + | Dpe Del Dp])'; | ||
| + | |||
| + | tauExtr= tauIst-2*tauChip:4*tauChip/1000:tauIst+2*tauChip; | ||
| + | NtauExtr = length(tauExtr); | ||
| + | |||
| + | EpsPhi = 1*rand(1,1)*2*pi; | ||
| + | EpsW = 1*10*2*pi; | ||
| + | |||
| + | SdTeor = 2*qcno*Tc*stdn_IQ^2*sinc(EpsW*Tc/2 /pi)^2*(4/tauChip - 2*(deltaTau/tauChip^2)); % Теоретическая крутизна | ||
| + | |||
| + | Ud = zeros(1,NtauExtr); | ||
| + | Udteor = zeros(1,NtauExtr); | ||
| + | |||
| + | p = nan(1,NtauExtr); | ||
| + | p_early = nan(1,NtauExtr); | ||
| + | p_late = nan(1,NtauExtr); | ||
| + | EpsTau = nan(1,NtauExtr); | ||
| + | Du_sim = zeros(1, length(qcno)); | ||
| + | Du_teor = nan(1, length(qcno)); | ||
| + | |||
| + | for q = 1:length(qcno) | ||
| + | EpsTau = 0; | ||
| + | |||
| + | p = ro(EpsTau); | ||
| + | p_late = ro(EpsTau+deltaTau/2); | ||
| + | p_early = ro(EpsTau-deltaTau/2); | ||
| + | |||
| + | for n = 1:Np | ||
| + | |||
| + | nI = L * randn(3,1); % Применяем результат разложения Холецкого и получаем коррелированные шумы | ||
| + | nQ = L* randn(3,1); | ||
| + | |||
| + | mI = A_IQ(q) * p * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | mIe = A_IQ(q)*p_early * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | mIl = A_IQ(q)*p_late *sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | |||
| + | mQ = -A_IQ(q) * p * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | mQe = -A_IQ(q)*p_early * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | mQl = -A_IQ(q)*p_late * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | |||
| + | I = mI + NoiseEnable*nI(1,1); | ||
| + | Ie = mIe + NoiseEnable*nI(2,1); | ||
| + | Il = mIl + NoiseEnable*nI(3,1); | ||
| + | Q = mQ + NoiseEnable*nQ(1,1); | ||
| + | Qe = mQe + NoiseEnable*nQ(2,1); | ||
| + | Ql = mQl + NoiseEnable*nQ(3,1); | ||
| + | |||
| + | udtau = -(Ie^2+Qe^2) + (Il^2+Ql^2); | ||
| + | Du_sim(q) = Du_sim(q) + udtau^2; | ||
| + | end | ||
| + | Du_sim(q) = Du_sim(q) / Np; | ||
| + | |||
| + | r1 = ro(deltaTau/2); | ||
| + | r2 = ro(2*deltaTau/2); | ||
| + | Du_teor(q) = (1 - r2) * 16 * qcno(q) * Tc * stdn_IQ^4 * (r1^2 + ((1 + r2) / (2 * qcno(q) * Tc))); | ||
| + | |||
| + | Du_norm = (4 * (1 - r2) * (r1^2 + ((1 + r2) / (2 * qcno(q) * Tc))))./... | ||
| + | ((2*qcno(q)*Tc*(2/tauChip - (deltaTau/tauChip^2))^2)); | ||
| + | end | ||
| + | % Du_norm = Du_teor./SdTeor.^2; | ||
| + | spec_sim = ['BPSK(1), \Delta=' sprintf('%.2f', deltaTau/tauChip) ' simul']; | ||
| + | spec_analit = ['BPSK(1), \Delta=' sprintf('%.2f', deltaTau/tauChip) ' analit']; | ||
| + | set(0,'DefaultAxesFontSize', 14) | ||
| + | |||
| + | figure(1) | ||
| + | li = plot(qcno_dB, sqrt(Du_sim)); hold on; | ||
| + | plot(qcno_dB, sqrt(Du_teor), '--', 'Color', li.Color) | ||
| + | legend(spec_sim, spec_analit); | ||
| + | xlabel('q_{c/n0}, dBHz', 'FontSize', 14) | ||
| + | ylabel('RMS ud noise', 'FontSize', 14); | ||
| + | grid on | ||
| + | |||
| + | figure(2) | ||
| + | li = plot(qcno_dB, LightC*sqrt(Du_sim)./SdTeor); hold on; | ||
| + | plot(qcno_dB, LightC*sqrt(Du_teor)./SdTeor, '--', 'Color', li.Color); hold on; | ||
| + | % plot(qcno_dB, LightC*sqrt(Du_norm), '--'); hold on; % дисперсия эквивалентных наблюдений | ||
| + | legend(spec_sim, spec_analit); | ||
| + | xlabel('q_{c/n0}, dBHz', 'FontSize', 14) | ||
| + | ylabel('RMS \delta \tau, m', 'FontSize', 14); | ||
| + | grid on | ||
| + | </source> | ||
| + | |frame-style = border:1px solid Plum | ||
| + | |title-style = color:black;background-color:lavender;text-align:left;font-weight:bold | ||
| + | |content-style = color:black;background-color:ghostwhite;text-align:center | ||
| + | |hidden = 1 | ||
| + | |footer = | ||
| + | |footer-style = background-color:lightgray;text-align:right | ||
| + | }} | ||
| + | |||
| + | |||
| + | [[Категория:Дискриминаторы]] | ||
Текущая версия на 18:15, 11 мая 2020
[править] Описание дискриминатора
Non-coherent Early minus Late Power (NELP) - некогерентный дискриминатор задержки, описываемый следующим соотношением:
 ,
,
где
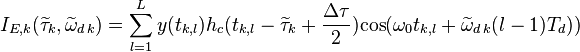 ,
,
 ,
,
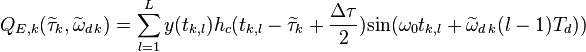 ,
,
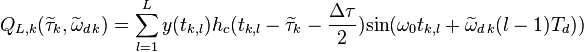 .
.
 - сдвиг дальномерного кода между запаздывающей и опережающей компонентами.
- сдвиг дальномерного кода между запаздывающей и опережающей компонентами.
[править] Дискриминационная характеристика
Дискриминационная характеристика описывается выражением (для квадратур с единичной дисперсией)
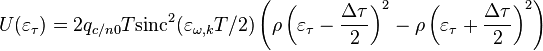 .
.
Ее крутизна 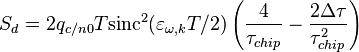 .
.
Для проверки формул составлена модель в Matlab.
В модели принято:
- длительность символа дальномерного кода
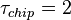 мкс,
мкс,
- расстройка по частоте
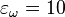 Гц,
Гц,
- каждая точка моделируемой дискриминационной характеристики усреднялась 1000 раз,
- корреляционная функция дальномерного кода соответствует сигналу с BPSK :
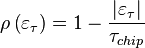 ;
;
- коррелированность шумов квадратур E, P, L моделируется с помощью разложения Холецкого.
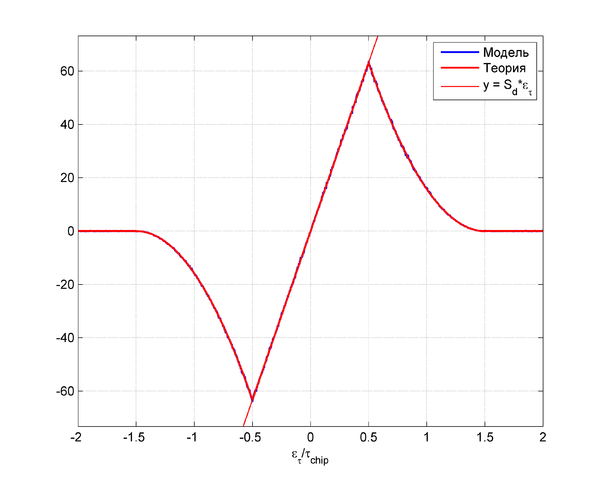
Результат моделирования для 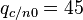 дБГц,
дБГц, 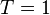 мс,
мс, 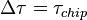 :
:
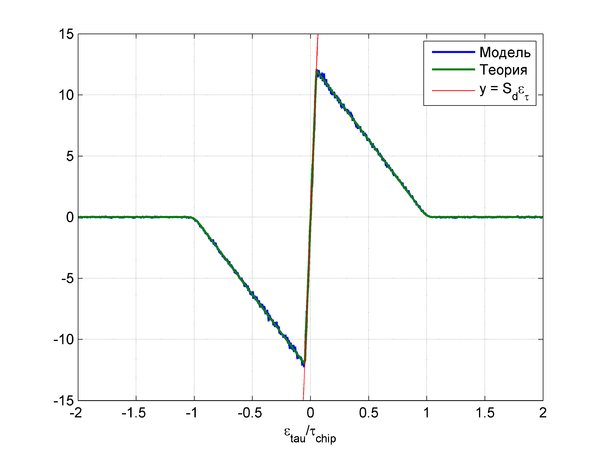
Результаты моделирования для 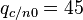 дБГц,
дБГц, 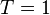 мс,
мс, 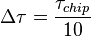 :
:
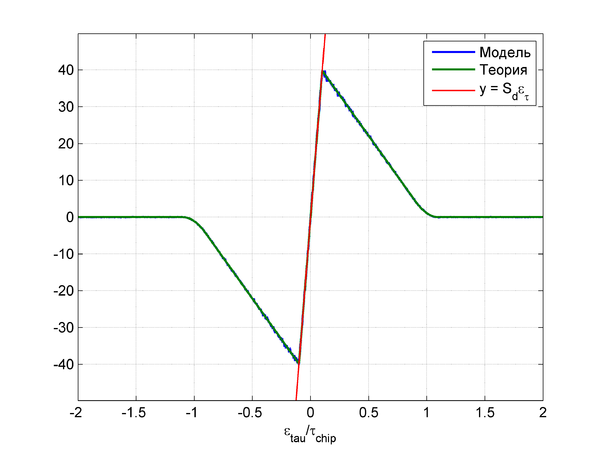
Результаты моделирования для  дБГц,
дБГц, 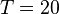 мс,
мс, 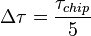 :
:
[править] Флуктуационная характеристика
Флуктуационная характеристика описывается выражением
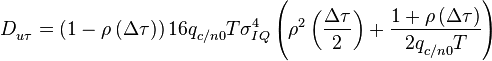 .
.
Дисперсия шума эквивалентного наблюдения, т.е. шума с выхода дискриминатора, пересчитанного к его входу при нулевой расстройке
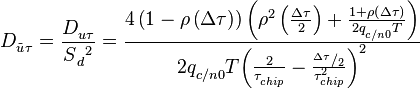
Аналитические выражения проверены на модели.
В модели принято:
- длительность символа дальномерного кода
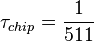 мс,
мс,
- время накопления коррелятора
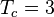 мс,
мс,
- усреднение проводилось по 5000 реализациям,
- расстройка по частоте
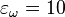 Гц,
Гц,
- корреляционная функция дальномерного кода соответствует сигналу с BPSK :
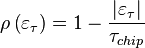 ;
;
- коррелированность шумов квадратур E, P, L моделируется с помощью разложения Холецкого.
Результаты моделирования:
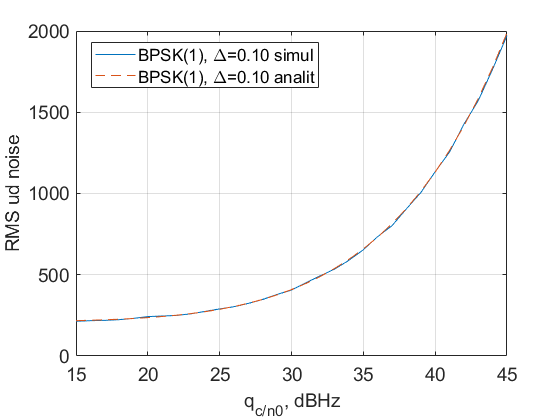
Зависимость СКО шума на выходе дискриминатора от отношения сигнал/шум при 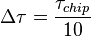 :
:
Зависимость СКО эквивалентных шумов от отношения сигнал/шум при 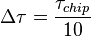 :
:
function r = ro( x )
global tauChip;
r = (abs(x) < tauChip).*(1 - abs(x)./tauChip);
end
Файл main.m
close all;
clear
clc
global tauChip
tauChip = 1e-3/511; % Длительность чипа
NoiseEnable = 1;
Np = 1000;
Tc = 0.001; % Период интегрирования в корреляторе
qcno_dB = 45;
stdn_IQ = 1; % СКО шума квадратурных сумм
qcno = 10^(qcno_dB/10);
A_IQ = stdn_IQ * sqrt(2 * qcno * Tc);
tauIst = tauChip/5;
deltaTau = tauChip/10;
Dp=stdn_IQ^2; % Дисперсия promt компоненты
Dpe=ro(deltaTau/2)*stdn_IQ^2; % Взаимная дисперсия promt-early/late
Del=ro(deltaTau)*stdn_IQ^2; % Взаимная дисперсия early-late
L=chol([Dp Dpe Dpe; % Используем разложение Холецкого
Dpe Dp Del;
Dpe Del Dp])';
tauExtr= [tauIst-2*tauChip:4*tauChip/1000:tauIst+2*tauChip];
NtauExtr = length(tauExtr);
EpsPhi = 1*rand(1,1)*2*pi;
EpsW = 1*10*2*pi;
SdTeor = 2*qcno*Tc*sinc(EpsW*Tc/2 /pi)^2*(4/tauChip - 2*(deltaTau/tauChip^2)); % Теоретическая крутизна
Ud = zeros(1,NtauExtr);
Udteor = zeros(1,NtauExtr);
p = nan(1,NtauExtr);
p_early = nan(1,NtauExtr);
p_late = nan(1,NtauExtr);
EpsTau = nan(1,NtauExtr);
for k = 1:NtauExtr
EpsTau(k) = tauIst - tauExtr(k);
p(k) = ro(EpsTau(k));
p_late(k) = ro(EpsTau(k)+deltaTau/2);
p_early(k) = ro(EpsTau(k)-deltaTau/2);
for n = 1:Np
nI = L * randn(3,1); % Применяем результат разложения Холецкого и получаем коррелированные шумы
nQ = L* randn(3,1);
mI = A_IQ * p(k) * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi);
mIe = A_IQ*p_early(k) * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi);
mIl = A_IQ*p_late(k) *sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi);
mQ = -A_IQ * p(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi);
mQe = -A_IQ*p_early(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi);
mQl = -A_IQ*p_late(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi);
I = mI + NoiseEnable*nI(1,1);
Ie = mIe + NoiseEnable*nI(2,1);
Il = mIl + NoiseEnable*nI(3,1);
Q = mQ + NoiseEnable*nQ(1,1);
Qe = mQe + NoiseEnable*nQ(2,1);
Ql = mQl + NoiseEnable*nQ(3,1);
Ud(k) = Ud(k) + (Ie^2-Il^2) + (Qe^2-Ql^2);
end
Udteor(k) = 2*qcno*Tc*(sinc(EpsW*Tc/2 /pi)^2)*(p_early(k)^2 - p_late(k)^2);
if ~mod(k,100)
fprintf('Progress: %.2f %%\n', k*100/NtauExtr)
end
end
plot(EpsTa[[:File:20200511_dep_Du_Sd2_qcn0_NELP.png]]u/tauChip, [Ud/Np; Udteor; SdTeor*EpsTau])
xlabel('\epsilon_{tau}/\tau_{chip}')
ylim([min(Udteor)-10 max(Udteor)+10])
grid on
Файл fluct.m
close all; clear; clc
global tauChip
tauChip = 1e-3/511; % Длительность чипа
LightC = 3e8;
NoiseEnable = 1;
Np = 5000;
Tc = 3e-3; % Период интегрирования в корреляторе
qcno_dB = 15:1:45;
qcno = 10.^(qcno_dB/10);
stdn_IQ = 13; % СКО шума квадратурных сумм
A_IQ = stdn_IQ * sqrt(2 * qcno * Tc);
tauIst =tauChip*rand(1,1);
deltaTau = tauChip/10;
Dp=stdn_IQ^2; % Дисперсия promt компоненты
Dpe=ro(deltaTau/2)*stdn_IQ^2; % Взаимная дисперсия promt-early/late
Del=ro(deltaTau)*stdn_IQ^2; % Взаимная дисперсия early-late
L=chol([Dp Dpe Dpe; % Используем разложение Холецкого
Dpe Dp Del;
Dpe Del Dp])';
tauExtr= tauIst-2*tauChip:4*tauChip/1000:tauIst+2*tauChip;
NtauExtr = length(tauExtr);
EpsPhi = 1*rand(1,1)*2*pi;
EpsW = 1*10*2*pi;
SdTeor = 2*qcno*Tc*stdn_IQ^2*sinc(EpsW*Tc/2 /pi)^2*(4/tauChip - 2*(deltaTau/tauChip^2)); % Теоретическая крутизна
Ud = zeros(1,NtauExtr);
Udteor = zeros(1,NtauExtr);
p = nan(1,NtauExtr);
p_early = nan(1,NtauExtr);
p_late = nan(1,NtauExtr);
EpsTau = nan(1,NtauExtr);
Du_sim = zeros(1, length(qcno));
Du_teor = nan(1, length(qcno));
for q = 1:length(qcno)
EpsTau = 0;
p = ro(EpsTau);
p_late = ro(EpsTau+deltaTau/2);
p_early = ro(EpsTau-deltaTau/2);
for n = 1:Np
nI = L * randn(3,1); % Применяем результат разложения Холецкого и получаем коррелированные шумы
nQ = L* randn(3,1);
mI = A_IQ(q) * p * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi);
mIe = A_IQ(q)*p_early * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi);
mIl = A_IQ(q)*p_late *sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi);
mQ = -A_IQ(q) * p * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi);
mQe = -A_IQ(q)*p_early * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi);
mQl = -A_IQ(q)*p_late * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi);
I = mI + NoiseEnable*nI(1,1);
Ie = mIe + NoiseEnable*nI(2,1);
Il = mIl + NoiseEnable*nI(3,1);
Q = mQ + NoiseEnable*nQ(1,1);
Qe = mQe + NoiseEnable*nQ(2,1);
Ql = mQl + NoiseEnable*nQ(3,1);
udtau = -(Ie^2+Qe^2) + (Il^2+Ql^2);
Du_sim(q) = Du_sim(q) + udtau^2;
end
Du_sim(q) = Du_sim(q) / Np;
r1 = ro(deltaTau/2);
r2 = ro(2*deltaTau/2);
Du_teor(q) = (1 - r2) * 16 * qcno(q) * Tc * stdn_IQ^4 * (r1^2 + ((1 + r2) / (2 * qcno(q) * Tc)));
Du_norm = (4 * (1 - r2) * (r1^2 + ((1 + r2) / (2 * qcno(q) * Tc))))./...
((2*qcno(q)*Tc*(2/tauChip - (deltaTau/tauChip^2))^2));
end
% Du_norm = Du_teor./SdTeor.^2;
spec_sim = ['BPSK(1), \Delta=' sprintf('%.2f', deltaTau/tauChip) ' simul'];
spec_analit = ['BPSK(1), \Delta=' sprintf('%.2f', deltaTau/tauChip) ' analit'];
set(0,'DefaultAxesFontSize', 14)
figure(1)
li = plot(qcno_dB, sqrt(Du_sim)); hold on;
plot(qcno_dB, sqrt(Du_teor), '--', 'Color', li.Color)
legend(spec_sim, spec_analit);
xlabel('q_{c/n0}, dBHz', 'FontSize', 14)
ylabel('RMS ud noise', 'FontSize', 14);
grid on
figure(2)
li = plot(qcno_dB, LightC*sqrt(Du_sim)./SdTeor); hold on;
plot(qcno_dB, LightC*sqrt(Du_teor)./SdTeor, '--', 'Color', li.Color); hold on;
% plot(qcno_dB, LightC*sqrt(Du_norm), '--'); hold on; % дисперсия эквивалентных наблюдений
legend(spec_sim, spec_analit);
xlabel('q_{c/n0}, dBHz', 'FontSize', 14)
ylabel('RMS \delta \tau, m', 'FontSize', 14);
grid on